
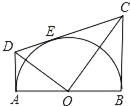
【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:
①OD2=DECD;②AD+BC=CD;③OD=OC;④S梯形ABCD=![]() CDOA;⑤∠DOC=90°,
CDOA;⑤∠DOC=90°,
其中正确的是_____.(只需填上正确结论的序号)
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是 “书”的概率为__________.
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.

(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数y=mx2+3mx﹣![]() m的图象与x轴交于A,B两点(点A在点B的左侧),顶点D和点B关于过点A的直线l:y=﹣
m的图象与x轴交于A,B两点(点A在点B的左侧),顶点D和点B关于过点A的直线l:y=﹣![]() x﹣
x﹣![]() 对称.
对称.
(1)求A、B两点的坐标及二次函数解析式;
(2)如图2,作直线AD,过点B作AD的平行线交直线1于点E,若点P是直线AD上的一动点,点Q是直线AE上的一动点.连接DQ、QP、PE,试求DQ+QP+PE的最小值;若不存在,请说明理由:
(3)将二次函数图象向右平移![]() 个单位,再向上平移3
个单位,再向上平移3![]() 个单位,平移后的二次函数图象上存在一点M,其横坐标为3,在y轴上是否存在点F,使得∠MAF=45°?若存在,请求出点F坐标;若不存在,请说明理由.
个单位,平移后的二次函数图象上存在一点M,其横坐标为3,在y轴上是否存在点F,使得∠MAF=45°?若存在,请求出点F坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
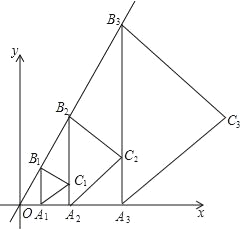
【题目】如图,点A1(1,0)在x轴上,过点A1作A1B1∥y轴交直线y=![]() x于点B1,以A1B1为边在A1B1的右侧作等边△A1B1C1,再过点C1作A2B2∥y轴,分别交直线x轴和直线y=
x于点B1,以A1B1为边在A1B1的右侧作等边△A1B1C1,再过点C1作A2B2∥y轴,分别交直线x轴和直线y=![]() x于A2,B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为_____(用含正整数n的代数式表示).
x于A2,B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为_____(用含正整数n的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com