练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如下图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),点B2019的坐标为_____

    【答案】（6058,0）

    【解析】

    首先根据已知求出三角形三边长度，然后通过旋转发现，B、B2、B4…每偶数之间的B相差6个单位长度，根据这个规律可以求得B2019的坐标．

    解：∵A（，0），B（0，2），
    ∴Rt△AOB中，AB=，
    ∴OA+AB1+B1C2=+2+=6，
    ∴B2的横坐标为：6，且B2C2=2，即B2（6，2），
    ∴B4的横坐标为：2×6=12，
    ∴点B2019的横坐标为：2018÷2×6++=6058，点B2019的纵坐标为：0，
    即B2019的坐标是（6058，0）．
    故答案为：（6058，0）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪，如平面几何图，AD=24m，∠D=90°，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°（tan31°≈0.6，tan50°≈1.2，结果精确到1m）.

    （1）求B，C的距离.

    （2）通过计算，判断此轿车是否超速.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2﹣4ax+3a．

    （Ⅰ）求该二次函数的对称轴；

    （Ⅱ）若该二次函数的图象开口向下，当1≤x≤4时，y的最大值是2，且当1≤x≤4时，函数图象的最高点为点P，最低点为点Q，求△OPQ的面积；

    （Ⅲ）若对于该抛物线上的两点P（x1，y1），Q（x2，y2），当t≤x1≤t+1，x2≥5时，均满足y1≥y2，请结合图象，直接写出t的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，下述结论：(1)BD平分∠ABC；(2)AD=BD=BC；(3)△BDC的周长等于AB+BC；(4)D是AC中点．其中正确的命题序号是（ ）

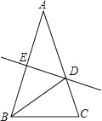
    A.4个B.3个C.2个D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线经过点A（，0），B（，0），且与y轴相交于点C．

    （1）求这条抛物线的表达式；

    （2）求∠ACB的度数；

    （3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为xh，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系，根据图象解决以下问题：

    （1）慢车的速度为_____km/h，快车的速度为_____km/h；

    （2）解释图中点C的实际意义并求出点C的坐标；

    （3）求当x为多少时，两车之间的距离为500km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2016广西贺州市）如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（　　）

    A. （2，5） B. （5，2） C. （2，﹣5） D. （5，﹣2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，.点在轴的正半轴上，边AB在轴上(点A在点B的左侧).

    (1)求点C的坐标.

    (2)点D是BC边上一点，点E是AB边上一点，且点E和点C关于AD所在直线对称，直接写出点D坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1,在平面直角坐标系中,A(5， 0), B(0， 5), C(2， 0),连AB

    (1)如图2，D为第一象限内一点，CDBC于点C,ADAB于点A,求点D坐标；

    (2)E为轴负半轴上一动点，连BE，在轴下方做EFBE于点E，并且EF=BE,连FC，直接写出当CF最短时点E的坐标.

    查看答案和解析>>

    同步练习册答案