
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 在
在![]() 轴的正半轴上,边AB在
轴的正半轴上,边AB在![]() 轴上(点A在点B的左侧).
轴上(点A在点B的左侧).
(1)求点C的坐标.
(2)点D是BC边上一点,点E是AB边上一点,且点E和点C关于AD所在直线对称,直接写出点D坐标.

 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数:________.
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为________和________,请用所学知识说明它们是一组勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),点B2019的坐标为_____
,0),B(0,2),点B2019的坐标为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某班数学兴趣小组利用数学知识测量建筑物DEFC的高度.他们从点A出发沿着坡度为i=1:2.4的斜坡AB步行26米到达点B处,此时测得建筑物顶端C的仰角α=35°,建筑物底端D的俯角β=30°.若AD为水平的地面,则此建筑物的高度CD约为( )米.(参考数据:![]() ≈1.7,tan35°≈0.7)
≈1.7,tan35°≈0.7)

A. 23.1 B. 21.9 C. 27.5 D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作![]() 交BC边于点F,联结EF.
交BC边于点F,联结EF.
(1)如图1,当![]() 时,求EF的长;
时,求EF的长;
(2)如图2,当点E在AC边上移动时, ![]() 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出![]() 的正切值;
的正切值;
(3)如图3,联结CD交EF于点Q,当![]() 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.
例如:[5.7]=5,[5]=5,[﹣1.5]=﹣2.
(1)[﹣![]() ]= ;
]= ;
(2)如果[a]=3,那么a的取值范围是 ;
(3)如果[![]() ]=﹣3,求满足条件的所有整数x.
]=﹣3,求满足条件的所有整数x.
查看答案和解析>>
科目:初中数学 来源: 题型:
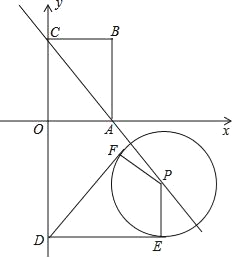
【题目】已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,﹣5),点P是直线AC上的一动点.
(1)当点P运动到线段AC的中点时,求直线DP的解析式(关系式);
(2)当点P沿直线AC移动时,过点D、P的直线与x轴交于点M.问在x轴的正半轴上是否存在使△DOM与△ABC相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)当点P沿直线AC移动时,以点P为圆心、R(R>0)为半径长画圆.得到的圆称为动圆P.若设动圆P的半径长为![]() ,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com