
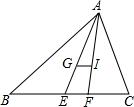
 在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.
在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论. 分析 连接AG、AI且延长分别交BC于D、E,连接IC,则AD为中线,AE、CI为角平分线.根据三角形重心的性质及GI∥BC可得到$\frac{AI}{IE}$=$\frac{AG}{GD}$.在△CAE中,利用相似三角形的性质定理易得到$\frac{AC}{CE}$=$\frac{AI}{IE}$,即AC=2CE.同理AB=2BE.得到AB+AC=2(BE+CE)=2BC.
解答 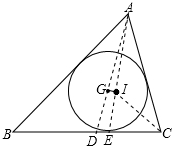 解:2a=b+c,证明如下:
解:2a=b+c,证明如下:
连接AG、AI且延长分别交BC于D、E,连接IC,则AD为中线,AE、CI为角平分线.
∵GI∥BC,
∴$\frac{AI}{IE}$=$\frac{AG}{GD}$=2.
在△CAE中,有$\frac{AC}{CE}$=$\frac{AI}{IE}$=2,即AC=2CE,
同理AB=2BE.
∴AB+AC=2(BE+CE)=2BC,
即2a=b+c.
点评 本题考查三角形的五心.本题综合性较强,考查知识点较深,是竞赛类题目的首选,解决本题的关键是掌握三角形五心的性质.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
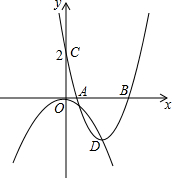 如图,已知抛物线C1:y=-$\frac{1}{2}$x2,平移抛物线y=x2,使其顶点D落在抛物线C1位于y轴右侧的图象上,设平移后的抛物线为C2,且C2与y轴交于点C(0,2).
如图,已知抛物线C1:y=-$\frac{1}{2}$x2,平移抛物线y=x2,使其顶点D落在抛物线C1位于y轴右侧的图象上,设平移后的抛物线为C2,且C2与y轴交于点C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个根,为x=±$\sqrt{n}$ | B. | 当n≥0时,有两个解,为x=±$\sqrt{n}$-m | ||
| C. | 当n≥0时,有两个解,为x=±$\sqrt{n-m}$ | D. | 当n≤0时,无实数解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com