
| A. | 有两个根,为x=±$\sqrt{n}$ | B. | 当n≥0时,有两个解,为x=±$\sqrt{n}$-m | ||
| C. | 当n≥0时,有两个解,为x=±$\sqrt{n-m}$ | D. | 当n≤0时,无实数解 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
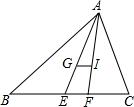 在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.
在△ABC中,BC=a,CA=b,AB=c,G与I分别是△ABC的重心和内心,若GI∥BC,请找出a、b、c之间的数量关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某个不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | $\left\{{\begin{array}{l}{x>1}\\{x>-2}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x≥1}\\{x>-2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x≤1}\\{x<-2}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x<1}\\{x<-2}\end{array}}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在边长为2的正方形ABCD中,分别以各顶点为圆心,在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分的外围的周长是2π.(结果保留π)
如图,在边长为2的正方形ABCD中,分别以各顶点为圆心,在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分的外围的周长是2π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com