
【题目】如图放置的两个正方形,大正方形![]() 边长为
边长为![]() ,小正方形
,小正方形![]() 边长为
边长为![]() (
(![]() ),
),![]() 在
在![]() 边上,且
边上,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 旋转至
旋转至![]() ,将
,将![]() 绕点
绕点![]() 旋转至
旋转至![]() ,给出以下五个结论:①
,给出以下五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 四点共圆,其中正确的序号为___________.
四点共圆,其中正确的序号为___________.
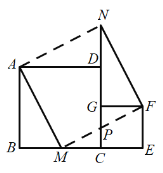
【答案】①③④⑤
【解析】
根据正方形的性质可得∠BAM+∠DAM=90°,∠NAD +∠AND=90°,然后根据旋转的性质可得∠NAD=∠BAM,从而判断①;证出![]() ∽
∽![]() ,列出比例式即可判断②;利用SAS即可证出③;先证出四边形AMFN是正方形,然后根据勾股定理即可判断④;证出∠AMP+∠ADP=180°,即可判断⑤.
,列出比例式即可判断②;利用SAS即可证出③;先证出四边形AMFN是正方形,然后根据勾股定理即可判断④;证出∠AMP+∠ADP=180°,即可判断⑤.
①∵四边形ABCD是正方形,
∴∠BAD=∠ADC=∠B=90°,
∴∠BAM+∠DAM=90°,∠NAD +∠AND=90°,
∵将![]() 绕点A旋转至
绕点A旋转至![]() ,
,
∴∠NAD=∠BAM,∠AND=∠AMB,
∴∠DAM=∠AND,故①正确;
②∵四边形CEFG是正方形,
∴PC∥EF,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),BM=b,
∴EF=b,CM=a﹣b,ME=(a﹣b)+b=a,
∴![]() ,
,
∴CP=![]() ;故②错误;
;故②错误;
③∵将![]() 绕点F旋转至
绕点F旋转至![]() ,
,
∴GN=ME,
∵AB=a,ME=a,
∴AB=ME=NG,
在![]() 与
与![]() 中,
中,
∵AB=NG=a,∠B=∠NGF=90°,GF=BM=b,
∴![]() ≌
≌![]() ;故③正确;
;故③正确;
④∵将![]() 绕点A旋转至
绕点A旋转至![]() ,
,
∴AM=AN,
∵将![]() 绕点F旋转至
绕点F旋转至![]() ,
,
∴NF=MF,
∵![]() ≌
≌![]() ,
,
∴AM=NF,
∴四边形AMFN是菱形,
∵∠BAM=∠NAD,
∴∠BAM+∠DAM=∠NAD+∠DAN=90°,
∴∠NAM=90°,
∴四边形AMFN是正方形,
∵在Rt![]() 中,a2+b2=AM2,
中,a2+b2=AM2,
∴S四边形AMFN=AM2=a2+b2;故④正确;
⑤∵四边形AMFN是正方形,
∴∠AMP=90°,
∵∠ADP=90°,
∴∠AMP+∠ADP=180°,
∴A,M,P,D四点共圆,故⑤正确.
综上:正确的结论有①③④⑤.
故答案为:①③④⑤.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE点F在AB上,且BF=DE
(1)求证:四边形BDEF是平行四边形
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某区1500名小学生和初中生的视力情况和他们每节课课间户外活动平均时长的统计图.
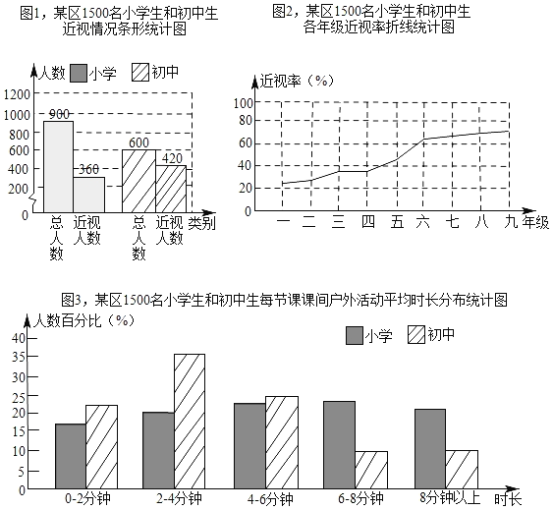
(1)根据图1,计算该区1500名学生的近视率;
(2)根据图2,从两个不同的角度描述该区1500名学生各年级近视率的变化趋势;
(3)根据图1、图2、图3,描述该区1500名学生近视率和所在学段(小学、初中)、每节课课间户外活动平均时长的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为直径的半圆
为直径的半圆![]() 按如图所示位置摆放,点
按如图所示位置摆放,点![]() 与点
与点![]() 重合,点
重合,点![]() 在边
在边![]() 的中点处,点
的中点处,点![]() 从现在的位置出发沿
从现在的位置出发沿![]() 方向以每秒2个单位长度的速度运动,点
方向以每秒2个单位长度的速度运动,点![]() 随之沿
随之沿![]() 下滑,并带动半圆
下滑,并带动半圆![]() 在平面内滑动,设运动时间为
在平面内滑动,设运动时间为![]() 秒(
秒(![]() ),点
),点![]() 运动到点
运动到点![]() 处停止,点
处停止,点![]() 为半圆中点.
为半圆中点.
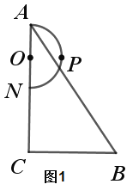
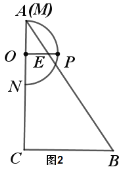
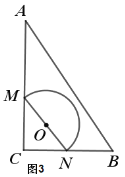
(1)如图2,当点![]() 与点
与点![]() 重合时,连接
重合时,连接![]() 交边
交边![]() 于
于![]() ,则
,则![]() 为____________;
为____________;
(2)如图3,当半圆的圆心![]() 落在了
落在了![]() 的斜边
的斜边![]() 的中线时,求此时的
的中线时,求此时的![]() ,并求出此时
,并求出此时![]() 的面积;
的面积;
(3)在整个运动的过程中,当半圆与边![]() 有两个公共点时,求出
有两个公共点时,求出![]() 的取值范围;
的取值范围;
(4)请直接写出在整个运动过程中点![]() 的运动路径长.
的运动路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,单位长度为![]() 的网格坐标系中,一次函数
的网格坐标系中,一次函数![]() 与坐标轴交于
与坐标轴交于![]() 、
、![]() 两点,反比例函数
两点,反比例函数![]()
![]() 经过一次函数上一点
经过一次函数上一点![]() .
.
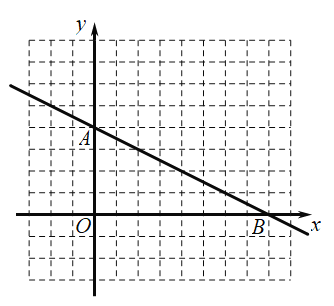
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于
交于![]() 、
、![]() 两点,在图中用直尺与
两点,在图中用直尺与![]() 铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点![]() 、点
、点![]() ;
;
②矩形的面积等于![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
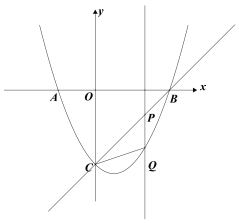
【题目】如图,抛物线y=![]() x2+mx+4m与x轴交于点A(
x2+mx+4m与x轴交于点A(![]() ,0)和点B(
,0)和点B(![]() ,0),与y轴交于点C,
,0),与y轴交于点C,![]() ,若对称轴在y轴的右侧.
,若对称轴在y轴的右侧.
(1)求抛物线的解析式
(2)在抛物线的对称轴上取一点M,使|MC-MB|的值最大;
(3)点Q是抛物线上任意一点,过点Q作PQ⊥x轴交直线BC于点P,连接CQ,当△CPQ是等腰三角形时,求点P的坐标.
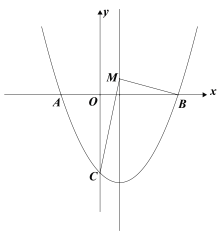
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何探究:
(问题发现)
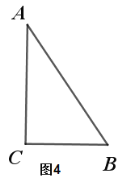
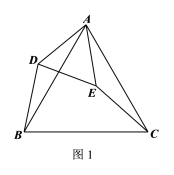
(1)如图1所示,△ABC和△ADE是有公共顶点的等边三角形,BD、CE的关系是_______(选填“相等”或“不相等”);(请直接写出答案)
(类比探究)
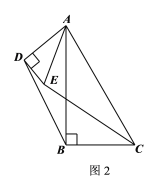
(2)如图2所示,△ABC和△ADE是有公共顶点的含有![]() 角的直角三角形,(1)中的结论还成立吗?请说明理由;
角的直角三角形,(1)中的结论还成立吗?请说明理由;
(拓展延伸)
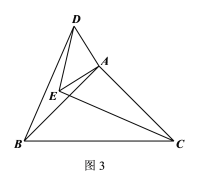
(3)如图3所示,△ADE和△ABC是有公共顶点且相似比为1 : 2的两个等腰直角三角形,将△ADE绕点A自由旋转,若![]() ,当B、D、E三点共线时,直接写出BD的长.
,当B、D、E三点共线时,直接写出BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
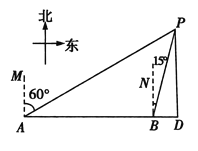
【题目】一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.
(1)求灯塔P到轮船航线的距离PD;(结果保留根号)
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里.(结果精确到1海里,参考数据![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
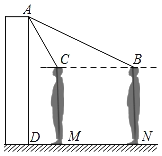
【题目】某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com