
【题目】如图,单位长度为![]() 的网格坐标系中,一次函数
的网格坐标系中,一次函数![]() 与坐标轴交于
与坐标轴交于![]() 、
、![]() 两点,反比例函数
两点,反比例函数![]()
![]() 经过一次函数上一点
经过一次函数上一点![]() .
.
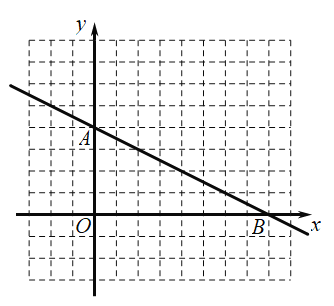
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于
交于![]() 、
、![]() 两点,在图中用直尺与
两点,在图中用直尺与![]() 铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
①四个顶点均在格点上,且其中两个顶点分别是点![]() 、点
、点![]() ;
;
②矩形的面积等于![]() 的值.
的值.
【答案】(1)![]() ,图形见解析;(2)
,图形见解析;(2)![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】
(1)由图可知A、B两点坐标,于是可以求出一次函数的解析式,反比例函经过一次函数上一点C,所以可以通过一次函数解析式求出C点坐标,既而求出反比例函数的解析式;明确反比例函数的解析式即可画出反比例函数图像.
(2)由图可知,一次函数与反比例函数相交于B、C两点,所以根据图像,当![]() 时,一次函数的y值大于反比例函数的y值.
时,一次函数的y值大于反比例函数的y值.
(3)根据题意,首先满足矩形的四个顶点均在格点上,其次,满足矩形的面积为10,先明确![]() 的值,然后要分两种情况讨论,分别是以
的值,然后要分两种情况讨论,分别是以![]() 为边和以
为边和以![]() 为对角线去思考画图即可.
为对角线去思考画图即可.
解(1)由图知点A坐标为(0,4),点B的坐标为(8,0),
一次函数![]() 经过A、B两点,∴
经过A、B两点,∴![]() ,
,
解得: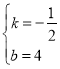 ,
,
∴一次函数解析式为:![]() ,
,
∵![]() 经过点C (2,a),
经过点C (2,a),
∴a=-1+4=3,
∴点C坐标为(2,3),
∵反比例函数![]() 经过点C(2,3),
经过点C(2,3),
∴![]() ,
,
∴反比例函数解析式为:![]() ;
;
当x=6时,y=1,所以反比例函数过D(6,1)
描绘出反比例函数![]() (x>0)的图像如下图:
(x>0)的图像如下图:
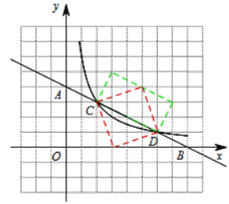
(2)由图可知,一次函数与反比例函数交于C、D两点,通过(1)得到C、D两点坐标,根据图中反比例函数与一次函数的位置关系,当![]() 时满足
时满足![]() .
.
故![]()
(3)画出两个以C、D为顶点的矩形如上图所示,理由如下:
由图像可知点C(2,3),点D(6,1),
依据勾股定理可得CD=![]() =
=![]() ,已知矩形面积为10的情况下,分类讨论:
,已知矩形面积为10的情况下,分类讨论:
若以CD为边构造矩形,则矩形的另一边为![]() ;
;
若以CD为对角线的情况下构造矩形,此时矩形为正方形,得其边长为![]() .
.
故构造符合题意的矩形共有3个.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是BC的中点,连接DE,P是DE上一点,∠BPC=90°,延长CP交AD于点F.⊙O经过P、D、F,交CD于点G.
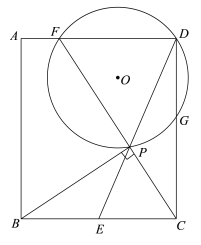
(1)求证:DF![]() DP;
DP;
(2)若![]() ,
,![]() ,求DG的长;
,求DG的长;
(3)连接BF,若BF是⊙O的切线,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
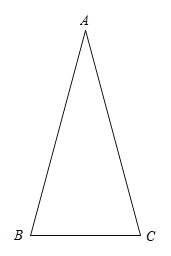
【题目】如图,在△ABC中,∠BAC=30°,AB=AC,将线段AC绕点A逆时针旋转α°(0<α<180),得到线段AD,连接BD,交AC于点P.
(1)当α=90时,
①依题意补全图形;
②求证:PD=2PB;
(2)写出一个α的值,使得PD=![]() PB成立,并证明.
PB成立,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
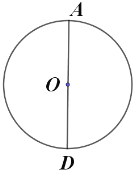
【题目】如图,![]() 为
为![]() 直径,作
直径,作![]() 的内接正六边形,甲、乙两人的作法分别如下:
的内接正六边形,甲、乙两人的作法分别如下:
甲:1.作![]() 的中垂线,交圆
的中垂线,交圆![]() 于
于![]() 两点;2.作
两点;2.作![]() 的中垂线,交圆
的中垂线,交圆![]() 于
于![]() 两点;3.顺次连接
两点;3.顺次连接![]() 六个点,六边形即为所求;
六个点,六边形即为所求;
乙:1.以![]() 为圆心,
为圆心,![]() 长为半径作弧,交圆
长为半径作弧,交圆![]() 于
于![]() 两点;2.以
两点;2.以![]() 为圆心,
为圆心,![]() 长为半径作弧,交圆
长为半径作弧,交圆![]() 于
于![]() 两点;3.顺次连接
两点;3.顺次连接![]() 六个点,六边形即为所求;
六个点,六边形即为所求;
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对B.甲不对,乙对
C.两人都不对D.两人都对
查看答案和解析>>
科目:初中数学 来源: 题型:
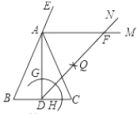
【题目】如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
A.6B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
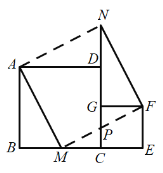
【题目】如图放置的两个正方形,大正方形![]() 边长为
边长为![]() ,小正方形
,小正方形![]() 边长为
边长为![]() (
(![]() ),
),![]() 在
在![]() 边上,且
边上,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 旋转至
旋转至![]() ,将
,将![]() 绕点
绕点![]() 旋转至
旋转至![]() ,给出以下五个结论:①
,给出以下五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 四点共圆,其中正确的序号为___________.
四点共圆,其中正确的序号为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,菱形ABCD如图所示,![]() ,点D在线段AB的垂直平分线上,若菱形ABCD绕点O逆时针旋转,旋转速度为每秒
,点D在线段AB的垂直平分线上,若菱形ABCD绕点O逆时针旋转,旋转速度为每秒![]() ,则第70秒时点D的对应坐标为( )
,则第70秒时点D的对应坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )
A.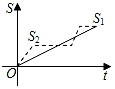 B.
B.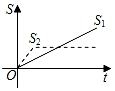
C.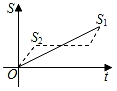 D.
D.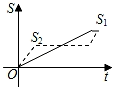
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com