
【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D﹣d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
A(﹣1,0)的距离跨度;
B( ![]() ,﹣
,﹣ ![]() )的距离跨度;
)的距离跨度;
C(﹣3,2)的距离跨度;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是 . 
(2)如图2,在平面直角坐标系xOy中,图形G2为以C(1,0)为圆心,2为半径的圆,直线y=k(x+1)上存在到G2的距离跨度为2的点,求k的取值范围. 
(3)如图3,在平面直角坐标系xOy中,射线OA:y= ![]() x(x≥0),圆C是以3为半径的圆,且圆心C在x轴上运动,若射线OA上存在点到圆C的距离跨度为2,直接写出圆心C的横坐标xc的取值范围.
x(x≥0),圆C是以3为半径的圆,且圆心C在x轴上运动,若射线OA上存在点到圆C的距离跨度为2,直接写出圆心C的横坐标xc的取值范围. 
【答案】
(1)1;3;2;圆
(2)解:设直线y=k(x+1)上存在到G2的距离跨度为2的点P(m,k(m+1)),
∴OP= ![]() ,
,
由(1)②知,圆内一点到图形圆的跨度是此点到圆心距离的2倍,圆外一点到图形圆的跨度是此圆的直径,
∵图形G2为以C(1,0)为圆心,2为半径的圆,到G2的距离跨度为2的点,
∴距离跨度小于图形G2的圆的直径4,
∴点P在图形G2⊙C内部,
∴R=2OP=2 ![]() ,
,
∵直线y=k(x+1)上存在到G2的距离跨度为2的点P,
∴2 ![]() =2,
=2,
∴(k2+1)m2+2(k2﹣1)m+k2=0①,
∵存在点P,
∴方程①有实数根,
∴△=4(k2﹣1)2﹣4×(k2+1)k2=﹣9k2+4≥0,
∴﹣ ![]()
(3)解:同(2)的方法得出,射线OA上存在点P到圆C的距离跨度为2时,点P在圆内,
设点P(n, ![]() n),(n>0),
n),(n>0),
∵圆心C(x2,0),∴PC= ![]() =
= ![]() ×2=1,
×2=1,
∴ ![]() n2﹣2x2n+x22﹣1=0,
n2﹣2x2n+x22﹣1=0,
∴射线OA上存在点到圆C的距离跨度为2,
∴ 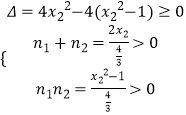 ,
,
∴1≤x2≤2
【解析】解:(1)如图1, 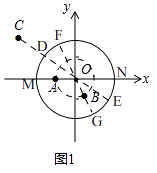
①∵图形G1为以O为圆心,2为半径的圆,∴直径为4,
∵A(﹣1,0),OA=1,
∴点A到⊙O的最小距离d=MA=OM﹣OA=1,
点A到⊙O的最大距离D=AN=ON+OM=2+1=3,
∴点A到图形G1的距离跨度R=D﹣d=3﹣1=2;
∵B( ![]() ,﹣
,﹣ ![]() ),∴OB=
),∴OB= ![]() =1,
=1,
∴点B到⊙O的最小距离d=BG=OG﹣OB=1,
点B到⊙O的最大距离D=BF=FO+OB=2+1=3,
∴点B到图形G1的距离跨度R=D﹣d=3﹣1=2;
∵C(﹣3,2),
∴OC= ![]() =
= ![]() ,
,
∴点C到⊙O的最小距离d=CD=OC﹣OD= ![]() ﹣2,
﹣2,
点C到⊙O的最大距离D=CE=OC+OE=2+ ![]()
∴点C到图形G1的距离跨度R=D﹣d=2+ ![]() ﹣(
﹣( ![]() ﹣2)=4;
﹣2)=4;
∴圆,
理由:①设⊙O内一点P的坐标为(x,y),
∴OP= ![]() ,
,
∴点P到⊙O的最小距离d=2﹣OP,点P到⊙O的最大距离D=2+OP,
∴点P到图形G1的距离跨度R=D﹣d=2+OP﹣(2﹣OP)=2OP;
∵图形G1的距离跨度为2,
∴2OP=2,
∴OP=1,
∴ ![]() =1,
=1,
∴x2+y2=1,
即:到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心,1为半径的圆.
②设⊙O外一点Q的坐标为(x,y),
∴OQ= ![]() ,
,
∴点Q到⊙O的最小距离d=OQ﹣2,点P到⊙O的最大距离D=OQ+2,
∴点P到图形G1的距离跨度R=D﹣d=OQ+2﹣(OQ﹣2)=4;
∵图形G1的距离跨度为2,
∴此种情况不存在,
所以,到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心,1为半径的圆.
故答案为:圆;
(1)①先根据跨度的定义先确定出点到圆的最小距离d和最大距离D,即可得出跨度;②分点在圆内和圆外两种情况同①的方法计算,判定得出结论;(2)先判断出存在的点P必在圆O内,设出点P的坐标,利用点P到圆心O的距离的2倍是点P到圆的距离跨度,建立方程,由于存在距离跨度是2的点,此方程有解即可得出k的范围.(3)同(2)方法判断出存在的点P在圆C内部,由于在射线OA上存在距离跨度是2的点,同(2)的方法建立方程,用一元二次方程根与系数的关系和根的判别式即可确定出范围.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图所示的是一个长![]() ,宽
,宽![]() ,高
,高![]() 的长方体,现在把它等分为
的长方体,现在把它等分为![]() 个棱长为
个棱长为![]() 的小正方体
的小正方体
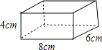
![]() 说明你的分法;
说明你的分法;
![]() 把这
把这![]() 个小正方体排成一排组成一个新长方体,这个新长方体与原长方体相比.表面积怎样变化?
个小正方体排成一排组成一个新长方体,这个新长方体与原长方体相比.表面积怎样变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.
![]()
(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校刚完成一批结构相同的学生宿舍的修建,这些宿舍地板需要铺瓷砖,一天4名一级技工去铺4个宿舍,结果还剩12 m2地面未铺瓷砖;同样时间内6名二级技工铺4个宿舍刚好完成,已知每名一级技工比二级技工一天多铺3 m2瓷砖.
(1)求每个宿舍需要铺瓷砖的地板面积.
(2)现该学校有20个宿舍的地板和36 m2的走廊需要铺瓷砖,某工程队有4名一级技工和6名二级技工,一开始有4名一级技工来铺瓷砖,3天后,学校根据实际情况要求2天后必须完成剩余的任务,所以决定加入一批二级技工一起工作,问需要再安排多少名二级技工才能按时完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,点(1,0)在函数图象上,那么abc、2a+b、a+b+c、a﹣b+c这四个代数式中,值大于或等于零的数有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是由些棱长![]() 的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).
的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).

查看答案和解析>>
科目:初中数学 来源: 题型:
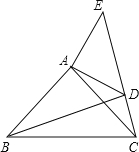
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC在平面直角坐标系中如图,已知AB=10,BC=8,EB是C上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() (k>0)与AB相交于点F,则线段AF的长为( )
(k>0)与AB相交于点F,则线段AF的长为( )
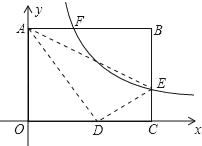
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com