
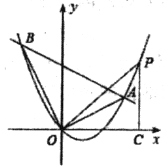
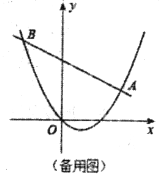
【题目】如图,在平面直角坐标系中抛物线![]() 经过原点,且与直线
经过原点,且与直线![]() 交于则
交于则![]() 、
、![]() 两点.
两点.
(1)求直线和抛物线的解析式;
(2)点![]() 在抛物线上,解决下列问题:
在抛物线上,解决下列问题:
①在直线![]() 下方的抛物线上求点
下方的抛物线上求点![]() ,使得
,使得![]() 的面积等于20;
的面积等于20;
②连接![]() ,作
,作![]() 轴于点
轴于点![]() ,若
,若![]() 和
和![]() 相似,请直接写出点
相似,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() 的坐标为
的坐标为![]() 或
或![]() ;②点
;②点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)把![]() 代入
代入![]() 即可求出一次函数解析式,把
即可求出一次函数解析式,把![]() 、
、![]() 代入
代入![]() 即可求出二次函数解析式;
即可求出二次函数解析式;
(2)①如图1,作![]() 轴,交
轴,交![]() 于点
于点![]() ,设
,设![]() ,则
,则![]() ,表示出PQ、AB的长,然后根据三角形的面积公式列式求解即可;
,表示出PQ、AB的长,然后根据三角形的面积公式列式求解即可;
②先根据勾股定理及其逆定理求出![]() ,然后分当
,然后分当![]() 时和当
时和当![]() 时两种情况求解即可.
时两种情况求解即可.
(1)把![]() 代入
代入![]() ,得
,得
![]() ,
,
![]() ,
,
![]() 直线解析式为
直线解析式为![]() ,
,
∵抛物线![]() 经过原点,
经过原点,
∴c=0.
把![]() 、
、![]() 代入
代入![]() ,得
,得
由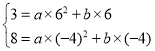 ,
,
得抛物线解析式为![]() ;
;
(2)①如图1,作![]() 轴,交
轴,交![]() 于点
于点![]() ,
,
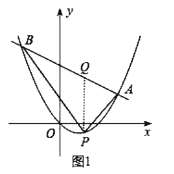
设![]() ,则
,则![]() ,
,
![]() ,AB=6+4=10,
,AB=6+4=10,
![]() ,
,
解得![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
②设![]() ,如图2,
,如图2,
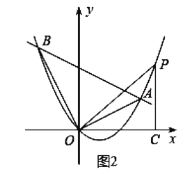
由题意得:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
即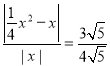 ,
,
整理得![]() ,
,
解方程![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;
;
解方程![]() 得
得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;
;
当![]() 时,
时,![]() ,即
,即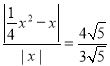 ,
,
整理得![]() ,
,
解方程![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标
点坐标![]() ;
;
解方程![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;
;
综上所述:点![]() 的坐标为:
的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
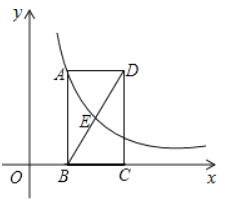
【题目】如图,已知点![]() 在函数
在函数![]() 的图象上,矩形
的图象上,矩形![]() 的边
的边![]() 在
在![]() 轴上,
轴上,![]() 是对角线
是对角线![]() 的中点,函数
的中点,函数![]() 的图象经过两点
的图象经过两点![]() ,
,![]() 点的横坐标为,点
点的横坐标为,点![]() 的横坐标为
的横坐标为![]() ,解答下列问题:
,解答下列问题:
(1)求反比例函数的解析式;
(2)求点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.
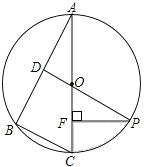
(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
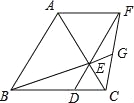
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.
考点:三角形综合题.
【题型】填空题
【结束】
19
【题目】先化简,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在创建全国文明城市过程中,决定购买A、B两种树苗对某路段道路进行绿化改造,已知购买A种树苗5棵,B种树苗3棵,需要840元;购买A种树苗3棵,B种树苗5棵,需要760元.
(1)求购买A、B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于30棵,且用于购买这两种树苗的资金不能超过10000元,现需购进这两种树苗共100棵,怎样购买所需资金最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并完成相关问题.
小明定义了一种新的运算,取名为※(加乘)运算.按这种运算进行运算的算式举例如下:
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;![]() .
.
问题:
(1)请归纳※(加乘)运算的运算法则:
两数进行※(加乘)运算时,________.特别地,0和任何数进行※(加乘)运算,或任何数和0进行※(加乘)运算,________.
(2)计算:![]() .(括号的作用与它在有理数运算中的作用一致)
.(括号的作用与它在有理数运算中的作用一致)
(3)我们知道加法有交换律和结合律,这两种运算律在有理数的※(加乘)运算中还适用吗?请任选一个运算律,判断它在※(加乘)运算中是否适用,并举例验证.(举一个例子即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
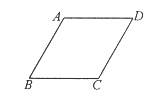
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是这个菱形内部或边上的一点,若以点
是这个菱形内部或边上的一点,若以点![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形,则
为顶点的三角形是等腰三角形,则![]() ,
,![]() (
(![]() ,
,![]() 两点不重合)两点间的最短距离为( )
两点不重合)两点间的最短距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,基灯塔AB建在陡峭的山坡上,该山坡的坡度i=1:0.75.小明为了测得灯塔的高度,他首先测得BC=20m,然后在C处水平向前走了34m到达一建筑物底部E处,他在该建筑物顶端F处测得灯塔顶端A的仰角为43°.若该建筑物EF=20m,则灯塔AB的高度约为(精确到0.1m,参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)( )
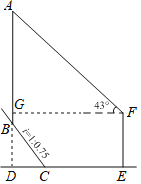
A.46.7mB.46.8mC.53.5mD.67.8m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com