
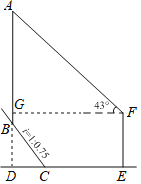
【题目】如图,基灯塔AB建在陡峭的山坡上,该山坡的坡度i=1:0.75.小明为了测得灯塔的高度,他首先测得BC=20m,然后在C处水平向前走了34m到达一建筑物底部E处,他在该建筑物顶端F处测得灯塔顶端A的仰角为43°.若该建筑物EF=20m,则灯塔AB的高度约为(精确到0.1m,参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)( )
A.46.7mB.46.8mC.53.5mD.67.8m
【答案】B
【解析】
根据山坡的坡度i=1:0.75,可得![]() =
=![]() ,设BD=4x,CD=3x,然后利用勾股定理求得BD=4x=16m,CD=3x=12m;再利用矩形的性质求出FG=DE=46m,BG=DG﹣DB=4m,最后利用三角函数解直角三角形即可.
,设BD=4x,CD=3x,然后利用勾股定理求得BD=4x=16m,CD=3x=12m;再利用矩形的性质求出FG=DE=46m,BG=DG﹣DB=4m,最后利用三角函数解直角三角形即可.
解:如图,∵∠ADC=90°,i=1:0.75,即![]() =
=![]() ,
,
∴设BD=4x,CD=3x,则BC=![]() =5x=20m,
=5x=20m,
解得:x=4,
∴BD=4x=16m,CD=3x=12m,
易得四边形DEFG是矩形,
则EF=DG=20m,FG=DE=DC+CE=12+34=46(m),
∴BG=DG﹣DB=4m,
在Rt△AFG中,AG=FG·tan∠AFG=46·tan43°≈46×0.93=42.78(m),
∴AB=AG+BG=42.78+4≈46.8(m),
故选:B.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
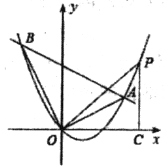
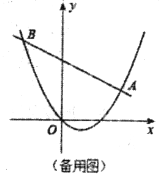
【题目】如图,在平面直角坐标系中抛物线![]() 经过原点,且与直线
经过原点,且与直线![]() 交于则
交于则![]() 、
、![]() 两点.
两点.
(1)求直线和抛物线的解析式;
(2)点![]() 在抛物线上,解决下列问题:
在抛物线上,解决下列问题:
①在直线![]() 下方的抛物线上求点
下方的抛物线上求点![]() ,使得
,使得![]() 的面积等于20;
的面积等于20;
②连接![]() ,作
,作![]() 轴于点
轴于点![]() ,若
,若![]() 和
和![]() 相似,请直接写出点
相似,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,P是BA延长线上一点,过点P作⊙O的切线,切点为D,连接BD,过点B作射线PD的垂线,垂足为C.

(1)求证:BD平分∠ABC;
(2)如果AB=6,sin∠CBD![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接国庆节,某工厂生产一种火爆的纪念商品,每件商品成本25元,工厂将该商品进行网络批发,批发单价![]() (元)与一次性批发量
(元)与一次性批发量![]() (件)(
(件)(![]() 为正整数)之间满足如图所示的函数关系.
为正整数)之间满足如图所示的函数关系.

(1)求![]() 与
与![]() 的函数解析式(也称关系式).
的函数解析式(也称关系式).
(2)若一次性批发量超过20且不超过50件时,求获得的利润![]() 与
与![]() 的函数关系式,同时求当批发量为多少件时,工厂获利最大?最大利润是多少?
的函数关系式,同时求当批发量为多少件时,工厂获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月17日是我国第6个扶贫日,也是第27个国际消除贫困日.为组织开展好铜陵市2019年扶贫日系列活动,促进我市贫困地区农产品销售,增加贫困群众收入,加快脱贫攻坚步伐.我市决定将一批铜陵生姜送往外地销售.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱生姜,且甲种货车装运1000箱生姜所用车辆与乙种货车装运800箱生姜所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少箱生姜?
(2)如果这批生姜有1520箱,用甲、乙两种汽车共16辆来装运,甲种车辆刚好装满,乙种车辆最后一辆只装了40箱,其它装满,求甲、乙两种货车各有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
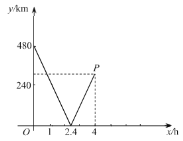
【题目】甲、乙两地之间有一条笔直的公路,快车和慢车分别从甲、乙两地同时出发,沿这条公路匀速相向而行,快车到达乙地后停止行驶,慢车到达甲地后停止行驶,已知快车速度为![]() .下图为两车之间的距离
.下图为两车之间的距离![]() 与慢车行驶时间
与慢车行驶时间![]() 的部分函数图像.
的部分函数图像.
(1)甲、乙两地之间的距离是______km;
(2)点![]() 的坐标为(4,____),解释点
的坐标为(4,____),解释点![]() 的实际意义.
的实际意义.
(3)根据题意,补全函数图像(标明必要的数据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数y=![]() 的图象交于点C(﹣1,m).
的图象交于点C(﹣1,m).
(1)求一次函数和反比例函数的表达式;
(2)直接写出关于x的不等式2x+b>![]() 的解集;
的解集;
(3)点P是这个反比例函数图象上的点,过点P作PM⊥x轴,垂足为点M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
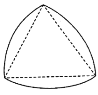
【题目】勒洛三角形是以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形,如图所示,若等边三角形的边长为1,则该勒洛三角形的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com