
����Ŀ�����Ķ����ٽ��
�������жϵ�(��7��20)�Ƿ���ֱ��y��2x��6��ʱ�����õķ����ǣ���x����7����y��2x��6�У���2��(��7)��6����8��20���жϳ���(��7��20)����ֱ��y��2x��6�ϣ�С���ɴ˷��������ݡ�����ȷ��һ��ֱ�ߡ����ƶϳ���A(1��2)��B(3��4)��C(��1��6)�������ȷ��һ��Բ������Ϊ�����ƶ���ȷ��?����������������˵�����ɣ�
���𰸡������ƶ�����ȷ�ģ������������.
�����������������Ҫ֤����![]() �����Ƿ����ȷ��һ��Բ����Ҫ��֤�����Ƿ���һ��ֱ���ϣ�������һ���Ƿ����㾭�����������ֱ�ߵĽ���ʽ��
�����Ƿ����ȷ��һ��Բ����Ҫ��֤�����Ƿ���һ��ֱ���ϣ�������һ���Ƿ����㾭�����������ֱ�ߵĽ���ʽ��
���������
�����ƶ�����ȷ�ģ�
��Ϊ������ȷ��һ��ֱ�������辭��A��B�����ֱ�ߵĽ���ʽΪy��kx��b��
��A(1��2)��B(3��4)����![]() ���
���![]()
�ྭ��A��B�����ֱ�ߵĽ���ʽΪy��x��1��
��x����1����y��x��1��
�ɣ�1��1��6����֪��C(��1��6)����ֱ��AB�ϣ�
��A��B��C���㲻��ͬһ��ֱ���ϣ�
����A��B��C�������ȷ��һ��Բ��


 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
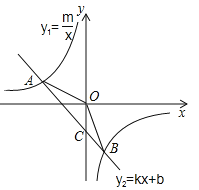
����Ŀ����ͼ����֪����������y1=![]() ��ͼ����һ�κ���y2=kx+b��ͼ��������A��-2,1����B��a��-2��.
��ͼ����һ�κ���y2=kx+b��ͼ��������A��-2,1����B��a��-2��.
��1������������һ�κ����Ľ���ʽ��
��2����һ�κ���y2=kx+b��ͼ��y���ڵ�C������AOB�������OΪ����ԭ�㣩��
��3����ʹy1��y2ʱx��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ�����Ҫ�������Ӧ������
�ڳ�����ѧ�α����ص�������ṫ��ʽ�������ù�ʽ��������ʽ�ֽ�ķ������������ù�ʽ��������ƽ���ʽ��a2-b2=��a+b����a-b������ȫƽ����ʽ��a2��2ab+b2=��a��b��2���зֽ���ʽ����������ȫƽ����ʽ�ֽ���ʽ�Ķ���ʽ����������ʽ��������������д������������ʽ����ƽ���͵���ʽ����һ����������������ʽ���Ļ���2������һ����������ʽ����ֱ��������ȫƽ����ʽ�ֽ���ʽʱ����Ӧ�����淽���ֽ���ʽ���Ƚ�����ʽax2+bx+c��a��0������Ϊa��x+m��2+n����ʽ�����ǰ������ı��η�����������ʽax2+bx+c���䷽���������ö���ʽ���䷽����ƽ���ʽ�ܶ�һЩ����ʽ���зֽ���ʽ��
���磺x2+8x+7
=x2+8x+16-16+7
=(x+4��2-9
=(x+4+3)(x+4-3)
=(x+7)(x+1)
�������ϲ��ϣ������Ӧ������
��1������������ʽ���䷽������x2+2x-3����a��x+m��2+n����ʽΪ_______��
��2��������������������ʽ�ֽ⣺
��x2+6x+8��
��x2-6x-7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Oֱ��AB����CD�ཻ�ڵ�E��AE=2��EB=6����DEB=30��������CD����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
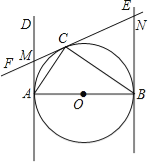
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��

��1����֤��OE=OF��
��2����CE=12��CF=5����OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABΪ��O��ֱ����AB=2��AD��BE��ԲO���������ߣ�A��BΪ�е㣬��Բ��һ��C����O������CF���ֱ�AD��BE�ڵ�M��N������AC��CB������ABC=30������AM= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
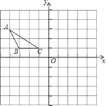
����Ŀ����֪����ͼ���ڡ�ABC�У���A������Ϊ����4��3������B������Ϊ����3��1����BC=2��BC��x��.
��1��������ABC����y��ԳƵ�ͼ�Ρ�A1B1C1����д��A1��B1��C1�����ꣻ
��2�����Ե�A��B��B1��A1Ϊ������ı��ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,ֱ��![]() ��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵڶ���������������ABCD����D��������_______����y������һ������M����
��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵڶ���������������ABCD����D��������_______����y������һ������M����![]() ���ܳ�ֵ��Сʱ���������Сֵ��_______��
���ܳ�ֵ��Сʱ���������Сֵ��_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪2a-1��a+5��m��ƽ��������m��ֵ��
��2����![]() ����������Ϊ
����������Ϊ![]() ��С������Ϊ
��С������Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��3����![]() ��|b��
��|b��![]() |��Ϊ�෴���������x�ķ���(2a��4)x2��b2��6��0.
|��Ϊ�෴���������x�ķ���(2a��4)x2��b2��6��0.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com