
【题目】如图,升降平台由三个边长为1.2米的菱形和两个腰长为1.2米的等腰三角形组成,其中平台AM与底座A0N平行,长度均为24米,点B,B0分别在AM和A0N上滑动这种设计是利用平行四边形的________;为了安全,该平台作业时∠B1不得超过60°,则平台高度(AA0)的最大值为________米

【答案】不稳定性; 4.8
【解析】
(1)根据四边形的不稳定性即可解决问题.
(2)当∠B1=60°时,平台AA0的高度最大,解直角三角形A1B0A0,可得A0A1的长,再由AA3=A3A2=A2A1=A1A0,即可解决问题.
解:(1)因为四边形具有不稳定性,点B,B0分别在AM和A0N上滑动 ,从而达到升降目的,因而这种设计利用了平行四边形的不稳定性;
(2)由图可知,当∠B1=60°时,平台AA0的高度最大,![]() =30°,B0A1=2A1C1=2.4,则A0A1=A1B0sin∠A1B0A0=2.4×
=30°,B0A1=2A1C1=2.4,则A0A1=A1B0sin∠A1B0A0=2.4×![]() =1.2.
=1.2.
又∵AA3=A3A2=A2A1=A1A0=1.2,则AA0=4×1.2=4.8.
故答案为:不稳定性,4.8.


科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班准备外出春游,有3名教师参加。有甲乙两家旅行社,其收费标准都一样,但都表示可以优惠师生.甲旅行社承诺:教师免费,学生按8折收费;乙旅行社承诺:师生一律按7折收费.
问:(1)如果由旅行社筹办春游活动,在什么条件下,两家旅行社所收费用相等.
(2)如果这个班有45名学生,选择哪家旅行社较恰当.请说明选择的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C的对角线 A1C和OB1交于点M1;以M1A1为对角线作第二个正方形A2A1B2M1,对角线A1M1和A2B2交于点M2;以M2A1为对角线作第三个正方形A3A1B3M2,对角线A1M2和A3B3交于点M3;……依此类推,这样作的第n 个正方形对角线交点Mn的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
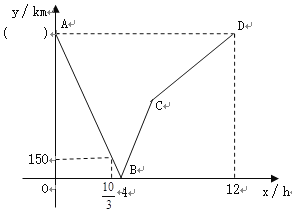
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图像回答以下问题:
(1)请在图中的( )内填上正确的值,并写出两车的速度和.
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接写出两车之间的距离不超过15km的时间范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
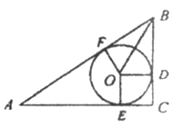
【题目】如图,在△ABC中,已知∠C=90°,BC=3,AC=4,⊙O是内切圆,E,F,D分别为切点,则tan∠OBD的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励市民节约用水,特制定如下的收费标准:若每月每户用水不超过10立方米,则按3元/立方米的水价收费,并加收0.2元/立方米的污水处理费;若超过10立方米,则超过的部分按4元/立方米的水价收费,污水处理费不变.
(1)若小华家5月份的用水量为8立方米,那么小华家5月份的水费为_______元;
(2)若小华家6月份的用水量为15立方米,那么小华家6月份的水费为_______元;
(3)若小华家某个月的用水量为a(a>10)立方米,求小华家这个月的水费(用含a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com