
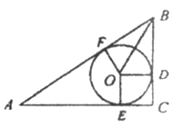
【题目】如图,在△ABC中,已知∠C=90°,BC=3,AC=4,⊙O是内切圆,E,F,D分别为切点,则tan∠OBD的值为___________.
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:

老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂。”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少。
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树。他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约_______千米。
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米。小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:

考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC与Rt△ABD中,![]() ,
,![]() ,AC、BD相交于点G,过点A作
,AC、BD相交于点G,过点A作![]() 交CB的延长线于点E,过点B作
交CB的延长线于点E,过点B作![]() 交DA的延长线于点F,AE、BF相交于点H.
交DA的延长线于点F,AE、BF相交于点H.

(1)证明:ΔABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校设计了如图所示的雕塑,取名“阶梯”, 现在工厂师傅打算用油漆喷刷所有暴露面,经测量,已知每个小立方体的棱长为0.5米.

(1)请你画出从它的正面、左面、上面三个不同方向看到的平面图形.
(2)请你帮助工人师傅计算一下,需要喷刷油漆的总面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,升降平台由三个边长为1.2米的菱形和两个腰长为1.2米的等腰三角形组成,其中平台AM与底座A0N平行,长度均为24米,点B,B0分别在AM和A0N上滑动这种设计是利用平行四边形的________;为了安全,该平台作业时∠B1不得超过60°,则平台高度(AA0)的最大值为________米

查看答案和解析>>
科目:初中数学 来源: 题型:
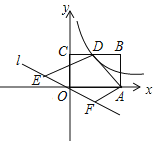
【题目】如图,函数y= ![]() (x>0)的图象与矩形OABC的边BC交于点D,分别过点A,D作AF∥DE,交直线y=k2x(k2<0)于点F,E.若OE=OF,BD=2CD,四边形ADEF的面积为12,则k1的值为________.
(x>0)的图象与矩形OABC的边BC交于点D,分别过点A,D作AF∥DE,交直线y=k2x(k2<0)于点F,E.若OE=OF,BD=2CD,四边形ADEF的面积为12,则k1的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有销售人员14人,为提高工作效率和员工的积极性,准备实行“每月定额销售,超额有奖”的措施.调查这14位销售人员某月的销售量,获得数据如下表:
月销售量(件) | 145 | 55 | 37 | 30 | 24 | 18 |
人数(人) | 1 | 1 | 2 | 5 | 3 | 2 |
(1)求这14位营销人员该月销售量的平均数和中位数
(2)如果你是该公司的销售部管理者,你将如何确定这个定额?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织七年级学生参加研学活动,如果单独租用45座客车若干辆,则刚好坐满;如果单独租用60座客车,则可少租1辆,并且剩余15个座位.
(1)求该校此次参加研学活动的学生有多少人?
(2)若单独租用60座的客车,需租_______辆;
(3)已知45座客车的日租金为每辆1 000元,60座客车的日租金为每辆1 200元,该校单独租用哪种车更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com