
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

【答案】(1)EC=2![]() ;(2)证明见解析;(3)2
;(2)证明见解析;(3)2
【解析】
(1)如图1,连接对角线BD,先证明△ABD是等边三角形,根据E是AB的中点,由等腰三角形三线合一得:DE⊥AB,利用勾股定理依次求DE和EC的长;
(2)如图2,作辅助线,构建全等三角形,先证明△ADH是等边三角形,再由△AMN是等边三角形,得条件证明△ANH≌△AMD(SAS),则HN=DM,根据DQ是△CHN的中位线,得HN=2DQ,由等量代换可得结论.
(3)先判断出点N在CD的延长线上时,CN+DM最小,最小为CH,再判断出∠ACD=30°,即可用三角函数求出结论.
(1)如图1,连接BD,则BD平分∠ABC,

∵四边形ABCD是菱形,
∴AD∥BC,
∴∠A+∠ABC=180,
∵∠A=60,
∴∠ABC=120,
∴ABD是等边三角形,
∴BD=AD=4,
∵E是AB的中点,
由勾股定理得:DE=2![]() ,
,
∵DC∥AB,
∴∠EDC=∠DEA=90,
在RtDEC中,
EC=2![]()
(2)如图2,延长CD至H,使CD=DH,连接NH、AH,
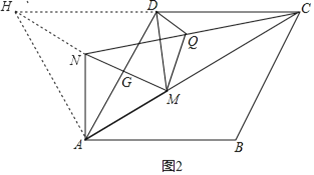
∵AD=CD,
∴AD=DH,
∵CD∥AB,
∴∠HDA=∠BAD=60,
∴ADH是等边三角形,
∴AH=AD, ∠HAD=60,
∵AMN是等边三角形,
∴AM=AN, ∠NAM=60,
∴∠HAN=∠DAM,
∴ANH≌AMD,
∴HN=DM,
∵D是CH的中点,Q是NC的中点,
∴DQ是CHN的中位线,
∴HN=2DQ,
∴DM=2DQ
(3) 如图2,由(2)知,HN=DM,
∴要CN+DM最小,便是CN+HN最小,
即:点C,H,N在同一条线上时,CN+DM最小,
此时,点D和点Q重合,
即:CN+DM的最小值为CH,
如图3,
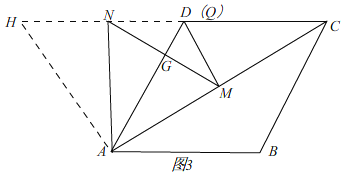
由(2)知,△ADH是等边三角形,
∴∠H=60°.
∵AC是菱形ABCD的对角线,
∴∠ACD=![]() ∠BCD=
∠BCD=![]() ∠BAD=30°,
∠BAD=30°,
∴∠CAH=180°-30°-60°=90°,
在Rt△ACH中,CH=![]() =2,
=2,
∴DM+CN的最小值为2.


科目:初中数学 来源: 题型:
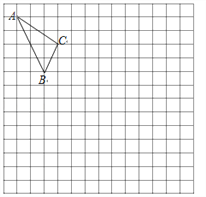
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.

(1)求k的值;
(2)如果点P在y轴上,且满足以点A、B、P为顶点的三角形是直角三角形,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
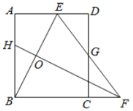
【题目】如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G.若G是CD的中点,则BC的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:

其中m=__________;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察函数图象,写出一条该函数的性质;
(4)进一步探究函数图象发现:
①方程![]() 有个互不相等的实数根;
有个互不相等的实数根;
②有两个点(x1,y1)和(x2,y2)在此函数图象上,当x2>x1>2时,比较y1和y2的大小关系为:
y1________y2 (填“>”、“<”或“=”);
③若关于x的方程![]() 有4个互不相等的实数根,则a的取值范围是________.
有4个互不相等的实数根,则a的取值范围是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:
①![]()
② -10 - (-31)
③1÷(﹣![]() )×
)×![]() ;
;
④(-2)2×5+(-2)3÷4
⑤![]()
(2)比较大小
①1.5与4 ②2与-7
③![]() 与
与![]() ④
④ ![]() 与
与![]()
(3)用简便方法计算:
①![]()
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=6,P为BC边上一点,△APD为等腰三角形.
(1)小明画出了一个满足条件的△APD,其中PA=PD,如图1所示,则tan ![]() 的值为 ;
的值为 ;
(2)请你在图2中再画出一个满足条件的△APD(与小明的不同),并求此时tan ![]() 的值.
的值.
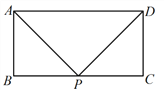

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=2,点P是线段AB上一点,分别以AP、BP为边作两个正方形.
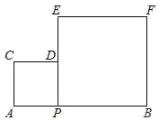
(1)如果APx,求两个正方形的面积之和S;
(2)当点P是AB的中点时,求两个正方形的面积之和S1;
(3)当点P不是AB的中点时,比较(1)中的S与(2)中S1的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF
(1) 在图中画出点O和△CDF,并简要说明作图过程
(2) 若AE=12,AB=13,求EF的长
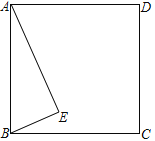
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com