
【题目】已知:如图,在平面直角坐标系xOy中,一次函数y=-x的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.

(1)求k的值;
(2)如果点P在y轴上,且满足以点A、B、P为顶点的三角形是直角三角形,直接写出点P的坐标.
【答案】(1)-1;(2)P点坐标为(0,![]() )、(0,-
)、(0,-![]() )、(0,2)、(0,-2).
)、(0,2)、(0,-2).
【解析】
试题分析:(1)首先求出A点坐标,再把A点坐标代入y=![]() 即可得到k的值;
即可得到k的值;
(2)BD⊥y轴,AC⊥y轴,如图,设P点坐标为(0,y),先根据对称得到B点坐标为(1,-1),再根据勾股定理得到AB2=22+22=8,PB2=PD2+BD2=(y+1)2+12,PA2=PC2+AC2=(y-1)2+12,然后分类讨论:当△APB是以AB为斜边的直角三角形,则PB2+PA2=AB2;当△APB是以PB为斜边的直角三角形,则AB2+PA2=PB2;当△APB是以PA为斜边的直角三角形,AB2+PB2=PA2,分别得到关于y的方程,解方程求出y的值即可得到P点坐标.
试题解析:(1)∵一次函数y=-x的图象与反比例函数y=![]() 的图象交于A、B两点,
的图象交于A、B两点,
根据图象可得出A点横坐标为-1,代入一次函数解析式,
∴y=-(-1)=1,
∴A点坐标为:(-1,1),
∵反比例函数y=![]() 的图象经过点A(-1,1),
的图象经过点A(-1,1),
∴k=-1×1=-1;
(2)作BD⊥y轴,AC⊥y轴,如图,设P点坐标为(0,y),
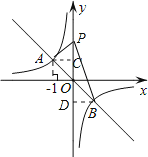
∵点A与B点关于原点对称,
∴B点坐标为(1,-1),
∴AB2=22+22=8,PB2=PD2+BD2=(y+1)2+12,PA2=PC2+AC2=(y-1)2+12,
分类:当△APB是以AB为斜边的直角三角形,则PB2+PA2=AB2,
∴PB2+PA2=AB2,即(y+1)2+12+(y-1)2+12=8,解得y=±![]() ;
;
当△APB是以PB为斜边的直角三角形,
∴AB2+PA2=PB2,即(y+1)2+12=(y-1)2+12+8,解得y=2;
当△APB是以PA为斜边的直角三角形,
∴AB2+PB2=PA2,即(y-1)2+12=(y+1)2+12+8,解得y=-2;
∴P点坐标为(0,![]() )、(0,-
)、(0,-![]() )、(0,2)、(0,-2).
)、(0,2)、(0,-2).


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列四个关于是否成反比例的命题,判断它们的真假.
(1)面积一定的等腰三角形的底边长和底边上的高成反比例;
(2)面积一定的菱形的两条对角线长成反比例;
(3)面积一定的矩形的两条对角线长成反比例;
(4)面积一定的直角三角形的两直角边长成比例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元/件的日用品。若按每件5元的价格出售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件;假定每月的销售件数y(万件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,王老师站在湖边度假村的景点A处,观察到一只水鸟由岸边D处飞向湖中小岛C处,点A到DC所在水平面的距离AB是15米,观测水鸟在点D和点C处时的俯角分别为53°和11°,求C、D两点之间距离.(精确到0.1.参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin11°≈0.19,cos11°≈0.98,tan11°≈0.19)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com