
(本题满分10分)已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.

(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
(1)见解析(5分)(2)菱形 证明:见解析(5分)
【解析】
试题分析:(1)根据条件证△ABE≌△ADF即可;(2)因为OA=OM,所以证明EF、AM互相垂直平分,从而可判定四边形AEMF是菱形.
试题解析:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,在Rt△ABE和Rt△ADF中,∵AD=AB,AF=AE,∴Rt△ADF≌Rt△ABE(HL)∴BE=DF;(2)【解析】
四边形AEMF是菱形,理由为:证明:∵四边形ABCD是正方形,∴∠BCA=∠DCA=45°,BC=DC,∵BE=DF,∴BC-BE=DC-DF,即CE=CF,在△COE和△COF中CE=CF,∠ACB=∠ACD, OC=OC∴△COE≌△COF(SAS),∴OE=OF,又OM=OA,∴四边形AEMF是平行四边形,∵AE=AF,∴平行四边形AEMF是菱形.
考点:1.正方形的性质;2.全等三角形的判定与性质;3. 菱形的判定.


科目:初中数学 来源:2014-2015学年安徽濉溪城关中心学校八年级上学期第三次月考数学卷(解析版) 题型:选择题
下图中表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)图象是 ( )
A. B.
B. C.
C.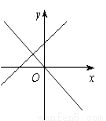 D.
D.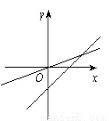
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期12月月考数学试卷(解析版) 题型:解答题
一条河的两岸有一段是平行的,在该河岸的这一段每隔5米有一棵树,河对岸每隔50米有一根电线杆.在这岸离开岸边25米的A处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,且这两棵树之间还有3棵树,求河的宽度.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期12月月考数学试卷(解析版) 题型:选择题
如图,在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有 ( )

A.ΔADE∽ΔAEF B. ΔECF∽ΔAEF
C.ΔADE∽ΔECF D. ΔAEF∽ΔABF
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期第三次教学质量监测数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).

(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期第三次教学质量监测数学试卷(解析版) 题型:填空题
如图,在半径为5cm的⊙O中,∠ ACB =300,则 的长度等于:
的长度等于:

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期第三次教学质量监测数学试卷(解析版) 题型:选择题
⊙O的半径为5cm,点A、B、C是直线a上的三点,OA、OB、OC的长度分别是5cm、4cm、7cm,则直线a与⊙O的位置关系是: ( )
A.相离 B.相切 C.相交 D.不能确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄三校八年级上学期12月月考数学试卷(解析版) 题型:解答题
(10分)如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D.

求证:(1)∠EDC=∠ECD
(2)OC=OD
(3)OE是线段CD的垂直平分线
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期期中考试数学试卷(解析版) 题型:选择题
下列数中:-8,2.7,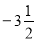 ,
,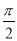 ,0.66666…,0,2,9.181181118……无理数的有( )
,0.66666…,0,2,9.181181118……无理数的有( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com