
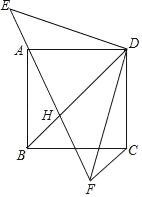
【题目】如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BD相交于点H,连接CF.
①求证:△DAE≌△DCF.
②求证:AH2=AE2+HF2.
【答案】①详见解析;②详见解析.
【解析】
由正方形ABCD与等腰直角三角形DEF,得到两对边相等,一对直角相等,利用SAS即可得证;
连接CH,求证△ADH≌△CDH和△ADE≌△CDF,再根据题目条件得出![]() 为直角三角形,即可求解.
为直角三角形,即可求解.
证明:①∵正方形ABCD,等腰直角三角形EDF,
∴∠ADC=∠EDF=90°,AD=CD,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
 ,
,
∴△ADE≌△CDF(SAS);
②连接CH,
∵DA=DC,∠ADH=∠CDH=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴AH=CH,
∵△ADE≌△CDF(SAS),
∴∠E=∠DFC=45°,
∵∠DFE=45°,
∴∠HFC=90°,
∴CH2=FH2+CF2,
∴AH2=FH2+CF2.


科目:初中数学 来源: 题型:
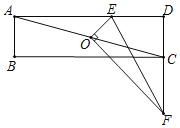
【题目】已知,O是矩形ABCD的对角线AC的中点,E是线段AD上的一点,作OF⊥OE于点O,交直线CD于点F,连结EF,若EF=2CF=2,则AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为宣传社会主义核心价值观,某社区居委会计划制作1200个大小相同的宣传栏.现有甲、乙两个广告公司都具备制作能力,居委会派出相关人员分别到这两个广告公司了解情况,获得如下信息:
信息一:甲公司单独制作完成这批宣传栏比乙公司单独制作完成这批宣传栏多用10天;
信息二:乙公司每天制作的数量是甲公司每天制作数量的1.2倍.
根据以上信息,求甲、乙两个广告公司每天分别能制作多少个宣传栏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
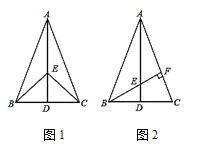
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,∠BAC=45°,原题设其他条件不变.求证:AB=BF+EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
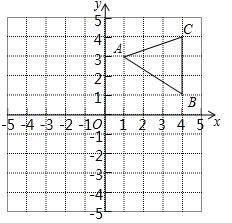
(1)请按要求画图:①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
(2)请写出直线B1C1与直线B2C2的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
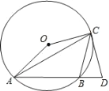
【题目】如图,△ABC是⊙O内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O切线交AB延长线于点D.
(1)求证:CD=CB;(2)如果⊙O的半径为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com