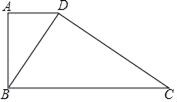
【题目】已知四边形ABCD中，∠BAD=∠BDC=90°，BD2=ADBC．
（1）求证：AD∥BC；
（2）过点A作AE∥CD交BC于点E．请完善图形并求证：CD2=BEBC．
【答案】（1）见解析；（2）见解析.
【解析】分析：（1）根据三角形的相似和平行线的性质可以证明结论成立；
（2）根据三角形的相似，对应边的比相等即可证明结论成立．
详解：（1）∵∠BAD=∠BDC=90°，BD2=ADBC，
∴
，∴△ADB∽△DBC，
∴∠ADB=∠DBC，∴AD∥BC；
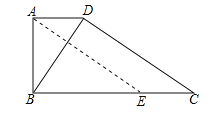
（2）如右图所示．
∵AD∥BC，AE∥DC，
∴四边形ADEC是平行四边形，∠AEB=∠BCD，∴AE=DC．
又∵∠BAD=∠BDC=90°，AD∥BC，
∴∠BAD+∠ABE=180°，∴∠ABE=90°，∴∠ABE=∠BDC，
∴△ABE∽△BDC，∴
，∴AEDC=BEBC．
∵AE=DC，∴CD2=BEBC．
综合自测系列答案科目：初中数学 来源： 题型：
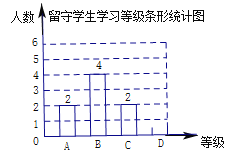
【题目】数学教师将班中留守学生的学习状况分成
四个等级，制成不完整的统计图：
（1）该班有多少名留守学生？并将该条形统计图补充完整．
（2）数学教师决定从
等级的留守学生中任选两名进行数学学习帮扶，使用列表或画树状图的方法，求出所选帮扶的两名留守学生来自同一等级的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
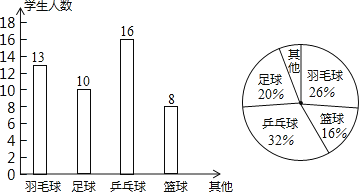
【题目】某校为了组织一次球类对抗赛，在本校随机抽取了若干名学生，对他们每个人最喜欢的一项球类运动进行了统计，将调查结果整理后绘制成如图所示的不完整的统计图，请你依据以上的信息回答下列问题：
（1）求本次被调查的学生人数；
（2）通过计算补全条形统计图；
（3）若全校有4000名学生，请你估计该校最喜欢篮球和足球运动的学生共有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB．
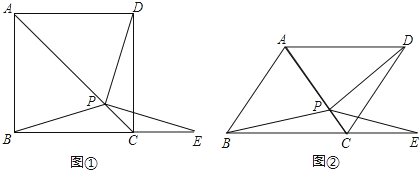
（1）求证：△BCP≌△DCP；
（2）求证：∠DPE=∠ABC；
（3）把正方形ABCD改为菱形，其它条件不变（如图②），若∠ABC=58°，则∠DPE= 度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某条道路上通行车辆限速60千米/时，道路的AB段为监测区，监测点P到AB的距离PH为50米（如图）．已知点P在点A的北偏东45°方向上，且在点B的北偏西60°方向上，点B在点A的北偏东75°方向上，那么车辆通过AB段的时间在多少秒以内，可认定为超速？（参考数据：
≈1.7，
≈1.4）．
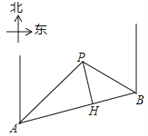
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1，3，则：
①ac＜0；②2a+b=0；③4a+2b+c＞0；④对于任意 x 均有 ax2+bx≥a+b，其中结论正确的个数有（ ）
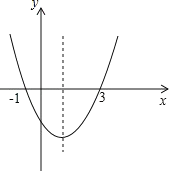
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现有正方形ABCD和一个以O为直角顶点的三角板，移动三角板，使三角板的两直角边所在直线分别与直线BC，CD交于点M，N．
（1）如图1，若点O与点A重合，则OM与ON的数量关系是__________________；
（2）如图2，若点O在正方形的中心（即两对角线的交点），则（1）中的结论是否仍然成立？请说明理由；
（3）如图3，若点O在正方形的内部（含边界），当OM=ON时，请探究点O在移动过程中可形成什么图形？
（4）如图4是点O在正方形外部的一种情况．当OM=ON时，请你就“点O的位置在各种情况下（含外部）移动所形成的图形”提出一个正确的结论．（不必说理）
查看答案和解析>>
科目：初中数学 来源： 题型：
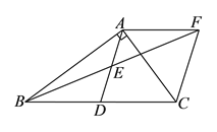
【题目】如图，在Rt△ABC中，BAC 90o，D是BC的中点，E是AD的中点，过点A作AF//BC 交 BE的延长线于点F，连接CF．
（1）求证：AD=AF．
（2）当AB=AC=
时，求四边形ADCF 的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，海中有一小岛P，在距小岛P的
海里范围内有暗礁，一轮船自西向东航行，它在A处时测得小岛P位于北偏东60°，且A、P之间的距离为32海里，若轮船继续向正东方向航行，轮船有无触礁危险？请通过计算加以说明．如果有危险，轮船自A处开始至少沿东偏南多少度方向航行，才能安全通过这一海域？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com