
分析 设P(x,2x-6),①如图1,当P在第一象限,作PH⊥x于H,由S△ACP=S梯形COHP-S△COA-S△PAH=4,列方程即可得到结果,②当P在第四象限,作PH⊥y轴于H,由S△APC+S△PHC=S△AOC+S梯形AOHP,列方程求得结果,③当P在第三象限,作PH⊥x轴于H,CN⊥y轴于N,由S△PNC+S△PAC=S梯形ACNH+S△PHA,列方程即可得到结果.
解答 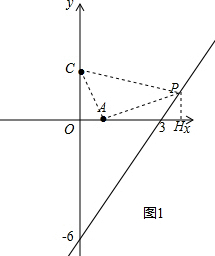 解:设P(x,2x-6),
解:设P(x,2x-6),
①如图1,当P在第一象限,作PH⊥x于H,
∴S△ACP=S梯形COHP-S△COA-S△PAH=4,
∴$\frac{1}{2}$(2x-6+2)•x-$\frac{1}{2}$×2×1-$\frac{1}{2}$(x-1)(2x-6)=4,
∴x=4,
∴y=2,
∴P(4,2);
②当P在第四象限,作PH⊥y轴于H,
∴CH=2-2x+6,PH=x,OH=-2x+6,
∴S△APC+S△PHC=S△AOC+S梯形AOHP,
∴4+$\frac{1}{2}$(2-2x+6)•x=$\frac{1}{2}$×2×1+$\frac{1}{2}$(1+z)(-2x+6),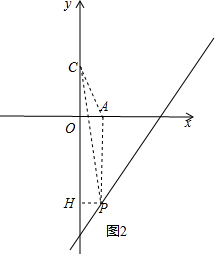
∴x=0,
∴y=-6,
∴P(0,-6);
③当P在第三象限,作PH⊥x轴于H,CN⊥y轴于N,
∴CN=-x,PH=-2x+6,PN=2-2x+6,AH=1-x,
∵S△PNC+S△PAC=S梯形ACNH+S△PHA,
∴$\frac{1}{2}$(-x)(2-2x+6)+4=$\frac{1}{2}$(-x+1-x)×2+$\frac{1}{2}$(1-x)(-2x+6),
∴x=0,
∴y=-6,
∴P(0,-6),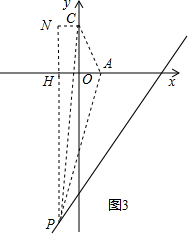
综上所述:P点的坐标(4,2),(0,-6).
点评 本题考查了一次函数图象上点的坐标特征,三角形的面积和梯形的面积的求法,正确的画出图形是解题的关键.


科目:初中数学 来源: 题型:选择题
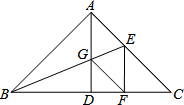 如图,AD为等腰直角三角形ABC斜边BC的中线,折叠△ABC,使AB落在BC上,点A恰好与BC上的点F重合,展开后,折痕BE分别交AC、AD于点E、G,连接GF.有下列四个结论:
如图,AD为等腰直角三角形ABC斜边BC的中线,折叠△ABC,使AB落在BC上,点A恰好与BC上的点F重合,展开后,折痕BE分别交AC、AD于点E、G,连接GF.有下列四个结论:| A. | ②③④ | B. | ①③④ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com