
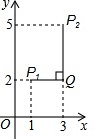
 在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:分析 ①根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0-y|=2,据此可以求得y的值;
②设点B的坐标为(0,y).因为|-$\frac{1}{2}$-0|≥|0-y|,所以点A与点B的“非常距离”最小值为|-$\frac{1}{2}$-0|=$\frac{1}{2}$.
解答 解:①∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|-$\frac{1}{2}$-0|=$\frac{1}{2}$≠2,
∴|0-y|=2,
解得,y=2或y=-2;
∴点B的坐标是(0,2)或(0,-2);
②点A与点B的“非常距离”的最小值为$\frac{1}{2}$.
点评 此题考查坐标与图形的特征,理解题意,掌握“非常距离”的求法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
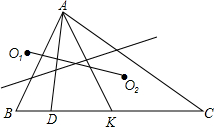 设D是△ABC的边BC上一点,但不是中点,设O1和O2分别是△ABD和△ADC的外心,求证:△ABC的中线AK的垂直平分线过线段O1O2中点.
设D是△ABC的边BC上一点,但不是中点,设O1和O2分别是△ABD和△ADC的外心,求证:△ABC的中线AK的垂直平分线过线段O1O2中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
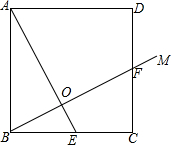 已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com