
【题目】已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.
(1)求证:BM=AC;
(2)求△ABC的面积.

【答案】(1)证明见解析;(2)14
【解析】试题分析:(1)由同角的余角相等,得到∠BME=∠C,再由△ABE是等腰直角三角形,得到AE=BE,即可证明△BEM≌△AEC,从而得到结论;
(2)由△BEM≌△AEC,得到BE、EM的长,进而得到BC的长,根据三角形面积公式即可求出结论.
试题解析:解:(1)∵AE、BD为△ABC的高, ∴∠BEM=∠AEC=∠BDC=90°,∴∠EBM+∠C=∠EBM+∠BME=90°, ∴∠BME=∠C.又∵∠ABC=45°,∴∠ABC=∠BAE=45°,∴AE=BE.在△BEM和△AEC中,∵∠BEM=∠AEC,∠BME=∠C,BE=AE,∴△BEM≌△AEC(AAS) ,∴BM=AC;
(2)∵△BEM≌△AEC,∴BE=AE=4,EM=EC=3,∴BC=BE+EC=7,∴△ABC的面积=![]() ×BC×AE=
×BC×AE=![]() ×7×4=14.
×7×4=14.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】以下调查中,适宜抽样调查的是( )
A.了解某班学生的身高情况
B.调查某批次汽车的抗撞击能力
C.了解全班同学每周体育锻炼的时间
D.对某校初三年级(2)班学生体能测试达标情况的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() 的解满足x<0,y>0.
的解满足x<0,y>0.
(1)x=________, y=________(用含a的代数式表示);
(2)求a的取值范围;
(3)若2x8y=2m,用含有a的代数式表示m,并求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
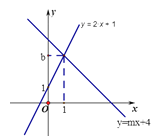
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,点
,点![]() 点
点![]() 分别在射线
分别在射线![]() ,射线
,射线![]() 上,若点
上,若点![]() 与点
与点![]() 关于
关于![]() 对称,点
对称,点![]() 点
点![]() 关于
关于![]() 对称,
对称, ![]() 与
与![]() 相交于点
相交于点![]() ,有以下命题:①
,有以下命题:①![]() ;②
;②![]() ;③若
;③若![]() ,
, ![]() ;④
;④![]() 是等腰直角三角形,则正确的命题有( ).
是等腰直角三角形,则正确的命题有( ).

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题.
例题:若![]() , 求m和n的值
, 求m和n的值
解:∵![]()
∴![]()
∴![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
问题:(1)若![]() ,求
,求![]() 的值.
的值.
(2)已知a,b,c是△ABC的三边长,满足![]() ,且c是△ABC中最长的边,求c的取值范围.
,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程 ![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围。
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com