
【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.
【答案】(1)200;(2)48;(3)1600
【解析】
(1)从统计图表中可得,“E组 其它”的频数为22,所占的百分比为11%,可求出调查学生总数;
(2)“开合跳”的人数占调查人数的24%,即可求出最喜爱“开合跳”的人数;
(3)求出“健身操”所占的百分比,用样本估计总体,即可求出8000人中喜爱“健身操”的人数.
解:(1)22÷11%=200.
∴参与问卷调查的学生总人数为200人.
(2)200×24%=48.
答:最喜爱“开合跳”的学生有48人.
(3)抽取学生中最喜爱“健身操”的初中学生有200-59-31-48-22=40(人),
![]() .
.
∴最喜爱“健身操”的初中学生人数约为1600人.


科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
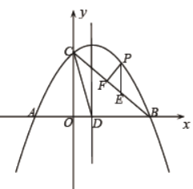
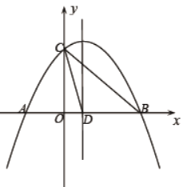
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,已知
,已知![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() .
.
备用图
(1)求该抛物线的解析式;
(2)连接![]() ,能否在抛物线上找到一点
,能否在抛物线上找到一点![]() ,使得
,使得![]() ,若有求
,若有求![]() 点的坐标,若没有说明理由;
点的坐标,若没有说明理由;
(3)若点![]() 为
为![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 的周长最大时,求点
的周长最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.

(1)当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.
(2)如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:
①其他条件不变,只要把活动调节点B向下移动即可,移动的距离BF与小华的身高DE有什么数量关系?直接写出你的结论;
②活动调节点B不动,只要调整α的大小,在图3中,试求α的度数.
(参考数据:![]() ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1cm,AC=BD=6cm, CE=DF, CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.
(1)当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是_____ cm.
(2)当夹子的开口最大(点C与点D重合)时,A,B两点的距离为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
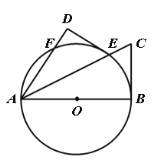
【题目】如图,已知AB是⊙O的直径,F是⊙O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若点G 为AE上一点,求OG+![]() EG最小值.
EG最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值
时,函数有最大值![]() .
.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象
图象![]() 轴下方部分沿
轴下方部分沿![]() 轴向上翻折,得到的新图象,若点
轴向上翻折,得到的新图象,若点![]() 是翻折得到的抛物线弧部分上任意一点,若关于
是翻折得到的抛物线弧部分上任意一点,若关于![]() 的一元二次方程
的一元二次方程![]() 恒有实数根时,求实数
恒有实数根时,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com