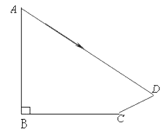
【题目】如图：学校旗杆附近有一斜坡．小明准备测量学校旗杆AB的高度，他发现当斜坡正对着太阳时，旗杆AB的影子恰好落在水平地面和斜坡的坡面上，此时小明测得水平地面上的影长BC=16米，斜坡坡面上的影长CD=10米，太阳光线AD与水平地面成30°角，斜坡CD与水平地面BC成30°的角，求旗杆AB的高度（结果保留根号）
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案科目：初中数学 来源： 题型：
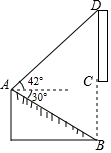
【题目】小婷在放学路上，看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD．她在A点测得标语牌顶端D处的仰角为42°，测得隧道底端B处的俯角为30°（B，C，D在同一条直线上），AB=10m，隧道高6.5m（即BC=65m），求标语牌CD的长（结果保留小数点后一位）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90，
≈1.73）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半径为2，圆心角为60°，则图中阴影部分的面积是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
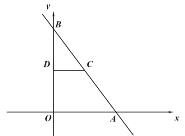
【题目】如图，在平面直角坐标系中，点
为坐标原点，直线
交
轴于点
，交
轴于点
，点
在
上，
，
，
交轴于点
．
（1）求点的坐标；
（2）点
从点出发，以每秒
个单位长度的速度沿
匀速运动，同时点
从点出发，以每秒
个单位长度的速度沿匀速运动，设点运动的时间为
秒
，
的面积为
，求与之间的函数关系式；
（3）在（2）的条件下，过点作
交轴于点
，连接
，点
为中点，连接
，求为何值时，直线
与轴相交所成的锐角与
互余．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，菱形OABC的顶点A的坐标为(5，0)，顶点B、C都在第一象限，对角线AC、BO交于点D，双曲线y=
（x＞0）经过点D，且ACBO40，则k的值为（ ）
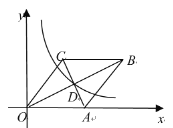
A.6B.8C.10D.12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】直线
如图所示，它与二次函数y＝ax2－2ax＋c的图像交于A、B两点（其中点A在点B的左侧），与这个二次函数图像的对称轴交于点C．
（1）求点C的坐标；
（2）设二次函数图像的顶点为D．若AD的垂直平分线经过点C，且
．求此二次函数的关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某企业生产的一种果汁饮料由A、B两种水果配制而成，其比例与成本如下方表格所示，已知该饮料的成本价为8元/千克，按现价售出后可获利润50%，每个月可出售27500瓶．
每千克饮料所占比例 | 成本（元/千克） | |
A | 20% | m |
B | 80% | m-15 |
（1）求m的值；
（2）由于物价上涨，A水果成本提高了25%，B水果成本提高了20%，在不改变售价的情况下，若要保持每个月的利润不减少，则现在至少需要售出多少瓶饮料？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
(m，n 为常数)．
（1）若抛物线的的对称轴为直线 x=1,且经过点（0，-1），求 m，n 的值；
（2）若抛物线上始终存在不重合的两点关于原点对称，求 n 的取值范围；
（3）在（1）的条件下，存在正实数 a，b( a＜b)，当 a≤x≤b 时，恰好有
，请直接写出 a，b 的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，抛物线
的顶点为点
，与
轴的负半轴交于点
，直线
交抛物线W于另一点
，点
的坐标为
．
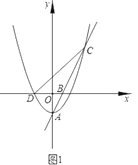
（1）求直线的解析式；
（2）过点作
轴，交轴于点
，若
平分
，求抛物线W的解析式；
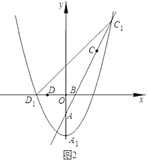
（3）若
，将抛物线W向下平移
个单位得到抛物线
，如图2，记抛物线的顶点为
，与轴负半轴的交点为
，与射线
的交点为
．问：在平移的过程中，
是否恒为定值？若是，请求出的值；若不是，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
