
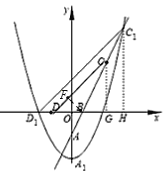
【题目】如图1,抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,直线
,直线![]() 交抛物线W于另一点
交抛物线W于另一点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
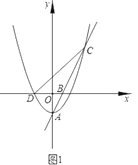
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,若
,若![]() 平分
平分![]() ,求抛物线W的解析式;
,求抛物线W的解析式;
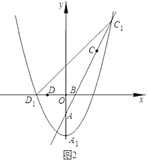
(3)若![]() ,将抛物线W向下平移
,将抛物线W向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,如图2,记抛物线
,如图2,记抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,与射线
,与射线![]() 的交点为
的交点为![]() .问:在平移的过程中,
.问:在平移的过程中,![]() 是否恒为定值?若是,请求出
是否恒为定值?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 恒为定值
恒为定值![]() .
.
【解析】
(1)由抛物线解析式可得顶点A坐标为(0,-2),利用待定系数法即可得直线AB解析式;
(2)如图,过点![]() 作
作![]() 于
于![]() ,根据角平分线的性质可得BE=BN,由∠BND=∠CED=90°,∠BND=∠CDE可证明
,根据角平分线的性质可得BE=BN,由∠BND=∠CED=90°,∠BND=∠CDE可证明![]() ,设BE=x,BD=y,根据相似三角形的性质可得CE=2x,CD=2y,根据勾股定理由得y与x的关系式,即可用含x的代数式表示出C、D坐标,代入y=ax2-2可得关于x、a的方程组,解方程组求出a值即可得答案;
,设BE=x,BD=y,根据相似三角形的性质可得CE=2x,CD=2y,根据勾股定理由得y与x的关系式,即可用含x的代数式表示出C、D坐标,代入y=ax2-2可得关于x、a的方程组,解方程组求出a值即可得答案;
(3)过点![]() 作
作![]() 于点
于点![]() ,根据平移规律可得抛物线W1的解析式为y=
,根据平移规律可得抛物线W1的解析式为y=![]() x2-2-m,设点
x2-2-m,设点![]() 的坐标为(t,0)(t<0),代入y=
的坐标为(t,0)(t<0),代入y=![]() x2-2-m可得2+m=
x2-2-m可得2+m=![]() t2,即可的W1的解析式为y=
t2,即可的W1的解析式为y=![]() x2-
x2-![]() t2,联立直线BC解析式可用含t的代数式表示出点C1的坐标,即可得
t2,联立直线BC解析式可用含t的代数式表示出点C1的坐标,即可得![]() ,可得∠
,可得∠![]() ,根据抛物线W的解析式可得点D坐标,联立直线BC与抛物线W的解析式可得点C、A坐标,即可求出CG、DG的长,可得CG=DG,∠CDG=∠
,根据抛物线W的解析式可得点D坐标,联立直线BC与抛物线W的解析式可得点C、A坐标,即可求出CG、DG的长,可得CG=DG,∠CDG=∠![]() ,即可证明
,即可证明![]() ,可得
,可得![]() ,
,![]() ,由∠CDG=45°可得BF=DF,根据等腰三角形的性质可求出DF的长,利用勾股定理可求出CD的长,即可求出CF的长,根据三角函数的定义即可得答案.
,由∠CDG=45°可得BF=DF,根据等腰三角形的性质可求出DF的长,利用勾股定理可求出CD的长,即可求出CF的长,根据三角函数的定义即可得答案.
(1)∵抛物线W:![]() 的顶点为点
的顶点为点![]() ,
,
∴点![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
∵B(1,0),
∴![]() ,
,
解得:![]() ,
,
∴抛物线解析式为:![]() .
.
(2)如图,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() 平分,
平分,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ,点
,点![]() ,
,
∴点![]() ,点
,点![]() 是抛物线W:
是抛物线W:![]() 上的点,
上的点,
∴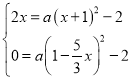 ,
,
∵x>0,
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为:![]() .
.
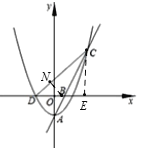
(3)![]() 恒为定值,理由如下:
恒为定值,理由如下:
如图,过点![]() 作
作![]() 轴于H,过点
轴于H,过点![]() 作
作![]() 轴G,过点
轴G,过点![]() 作
作![]() 于点
于点![]() ,
,
∵a=![]() ,
,
∴抛物线W的解析式为y=![]() x2-2,
x2-2,
∵将抛物线W向下平移m个单位,得到抛物线![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ,
,
∵抛物线![]() 与射线
与射线![]() 的交点为
的交点为![]() ,
,
∴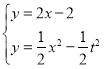 ,
,
解得: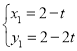 ,
,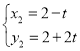 (不合题意舍去),
(不合题意舍去),
∴点![]() 的坐标
的坐标![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() 轴,
轴,
![]() ,
,
∵![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴点![]() ,
,
∵![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() ,
,
∴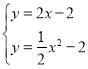 ,
,
解得:![]() 或
或![]() ,
,
∴点![]() ,A(0,-2),
,A(0,-2),
∴![]() ,
,
∴![]() ,且
,且![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() ,点
,点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 恒为定值.
恒为定值.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
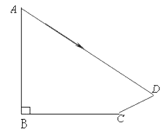
【题目】如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=16米,斜坡坡面上的影长CD=10米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列一元二次方程.
(1)(x+3)2﹣25=0;
(2)3(1+x)2=27;
(3)x2﹣4x+6=0;
(4)(x﹣1)(x+3)=12;
(5)3(x﹣2)2=x(x﹣2).
查看答案和解析>>
科目:初中数学 来源: 题型:
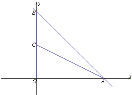
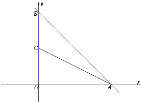
【题目】已知,平面直角坐标系中,直线y=-x+6交x轴于点A,交y轴于点B,点C为OB上一点,连接AC,且![]() ;
;
(1)求C点坐标;
(2)D为OC上一点,连接AD并延长至点E,连接OE、CE,取AE中点F,连接BF、OF,当F在第一象限时,求![]() 的值;
的值;
(3)在(2)的条件下,将射线AC延AE翻折交OE于点P,连接BP,过O作OH⊥AE于H,若AD=4FH,![]() ,求直线PB的解析式.
,求直线PB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为![]() 元
元![]() 件.试营销阶段发现:当销售单价是
件.试营销阶段发现:当销售单价是![]() 元时,每天的销售量为
元时,每天的销售量为![]() 件;销售单价每上涨
件;销售单价每上涨![]() 元,每天的销售量就减少
元,每天的销售量就减少![]() 件.
件.
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(2)当销售单价定为多少元时,该文具每天的销售利润最大?最大利润为多少元?
(3)商场的营销部结合上述情况,提出了![]() ,
,![]() 两种营销方案:
两种营销方案:
方案![]() :该文具的销售单价高于进价,但不超过
:该文具的销售单价高于进价,但不超过![]() 元;
元;
方案![]() :每天销售量不少于
:每天销售量不少于![]() 件,且每件文具的利润至少为
件,且每件文具的利润至少为![]() 元.
元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的变换点
的变换点![]() 的坐标定义如下:当
的坐标定义如下:当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ;当
;当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 的变换点
的变换点![]() 的坐标是_________;点
的坐标是_________;点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() __________
__________![]() ;
;
(2)若点![]() 是函数
是函数![]() 图象上的一点,点
图象上的一点,点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,求线段
,求线段![]() 长的取值范围;
长的取值范围;
(3)已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() .点
.点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 的变换点为
的变换点为![]() .若点
.若点![]() 恰好在抛物线的对称轴上,且四边形
恰好在抛物线的对称轴上,且四边形![]() 是菱形,求
是菱形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.

(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第![]() 天(
天(![]() 为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
时间 |
|
|
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) |
|
|
储存和损耗费用(元) |
|
|
已知该种水果的进价为4.1元/斤,设销售该水果第![]() (天)的利润为
(天)的利润为![]() (元),求
(元),求![]() 与
与![]() (
(![]() )之间的函数解析式,并求出第几天时销售利润最大.
)之间的函数解析式,并求出第几天时销售利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com