
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第![]() 天(
天(![]() 为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
时间 |
|
|
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) |
|
|
储存和损耗费用(元) |
|
|
已知该种水果的进价为4.1元/斤,设销售该水果第![]() (天)的利润为
(天)的利润为![]() (元),求
(元),求![]() 与
与![]() (
(![]() )之间的函数解析式,并求出第几天时销售利润最大.
)之间的函数解析式,并求出第几天时销售利润最大.
【答案】(1)10%;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;第10天时销售利润最大
;第10天时销售利润最大
【解析】
(1)设这个百分率是x,根据某商品原价为10元,由于各种原因连续两次降价,降价后的价格为8.1元,可列方程求解;
(2)根据两个取值先计算:当1≤x<9时和9≤x<15时销售单价,由利润=(售价-进价)×销量-费用列函数关系式,并根据增减性求最大值,作对比.
(1)设该种水果每次降价的百分率是![]() ,依题意,得:
,依题意,得:
![]()
解得![]() 或
或![]() (不符合题意,舍去),
(不符合题意,舍去),
答:该种水果每次降价的百分率是10%;
(2)当![]() 时,第1次降价后的价格:
时,第1次降价后的价格:![]() 元,
元,
∴![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() (元),
(元),
当![]() 时,第2次降价后的价格:8.1元,
时,第2次降价后的价格:8.1元,
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() (元)
(元)
∵380>334.3
∴第10天时销售利润最大;


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,直线
,直线![]() 交抛物线W于另一点
交抛物线W于另一点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
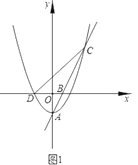
(1)求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,若
,若![]() 平分
平分![]() ,求抛物线W的解析式;
,求抛物线W的解析式;
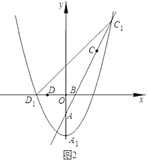
(3)若![]() ,将抛物线W向下平移
,将抛物线W向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,如图2,记抛物线
,如图2,记抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴负半轴的交点为
轴负半轴的交点为![]() ,与射线
,与射线![]() 的交点为
的交点为![]() .问:在平移的过程中,
.问:在平移的过程中,![]() 是否恒为定值?若是,请求出
是否恒为定值?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国杂粮看山西,山西杂粮看忻州,“忻州——中国杂粮之都”近年来打造以“一薯、三麦、四米、五豆”为特色的小杂粮产业,走上了“兴科技、树品牌、强产业广交流、共发展”的新道路.某县为帮助农民进一步提高杂粮播种水平,提升综合生产能力,决定财政拨款45600元购进A,B两种型号的播种机共30台.两种型号播种机的单价和工作效率分别如表:
单价/元 | 工作效率/(公顷/h) | |
A种型号 | 1600 | 4 |
B种型号 | 1480 | 3 |
(1)求购进A,B两种型号的播种机各多少台.
(2)某农场有2000公顷地种植杂粮,计划从县里新购进的播种机中租用两种型号的播种机共15台同时进行播种.若农场的工人每天工作8h,则至少租用A种型号的播种机多少台才能在5天内完成播种工作?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图 1、图 2 均是 6×6 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为 1,点 A、B、C、D 均在格点上.在图 1、图 2 中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
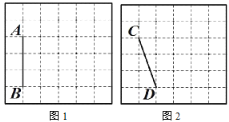
(1)在图 1 中以线段 AB 为边画一个△ABM,使∠ABM=45°,且△ABM 的面积为 6;
(2)在图 2 中以线段 CD 为边画一个四边形 CDEF,使∠CDE=∠CFE=90°,且四边形 CDEF 的面积为 8.
查看答案和解析>>
科目:初中数学 来源: 题型:
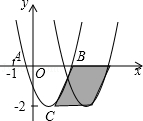
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)
①b>0
②a﹣b+c<0
③阴影部分的面积为4
④若c=﹣1,则b2=4a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .请按照要求写出符合条件的抛物线的解析式.
.请按照要求写出符合条件的抛物线的解析式.
(1)若抛物线![]() 与
与![]() 关于
关于![]() 轴对称,则
轴对称,则![]() = ;
= ;
(2)若抛物线![]() 与
与![]() 关于
关于![]() 轴对称,则
轴对称,则![]() = ;
= ;
(3)若抛物线![]() 与
与![]() 关于坐标原点对称,则
关于坐标原点对称,则![]() = ;
= ;
(4)若抛物线![]() 是由
是由![]() 绕着点P(1,0)旋转180°后所得,则
绕着点P(1,0)旋转180°后所得,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() ),销售量为
),销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①当
.该超市根据以往的销售经验得出以下的销售规律:①当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 与
与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)当![]() 时,
时,![]() 与
与![]() 的关系式为 ;
的关系式为 ;
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若超市希望第![]() 天到第
天到第![]() 天的日销售利润
天的日销售利润![]() (元)随
(元)随![]() 的增大而增大,则需要在当天销售价格的基础上涨
的增大而增大,则需要在当天销售价格的基础上涨![]() 元/
元/![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
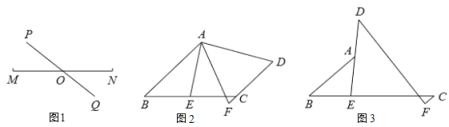
【题目】(1)操作:如图![]() ,点
,点![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() ,请利用图
,请利用图![]() 画出一对以点
画出一对以点![]() 为对称中心的全等三角形,(不写画法).
为对称中心的全等三角形,(不写画法).
根据上述操作得到的经验完成下列探究活动:
(2)探究一:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() 为
为![]() 边的中点,
边的中点,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,试探究线段
,试探究线段![]() 与
与![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.
(3)探究二,如图![]()
![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲投资销售一种利润率为0.4的电子产品,第一次购入的电子产品销售完后,甲取出28万元,并把剩下的本金和利润全部用于购入该电子产品;第二次购入的电子产品销售完后,再次取出19.6万元,并把剩下的本金和利润全部用于购入该电子产品;第三次购入电子产品销售完后,再次取出6.72万元.并把剩下的本金和利润全部用于购入该电子产品;第四次购入的电子产品销售完后,本次销售额为9.8万元,这样,甲投资该项目的本金和利润全部收回,则甲投资该项目的本金是_____万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com