
����Ŀ��ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ![]() Ԫ
Ԫ![]() ������Ӫ���η��֣������۵�����
������Ӫ���η��֣������۵�����![]() Ԫʱ��ÿ���������Ϊ
Ԫʱ��ÿ���������Ϊ![]() �������۵���ÿ����
�������۵���ÿ����![]() Ԫ��ÿ����������ͼ���
Ԫ��ÿ����������ͼ���![]() ����
����
��1��д���̳����������ľߣ�ÿ�����õ���������![]() (Ԫ)�����۵���
(Ԫ)�����۵���![]() (Ԫ)֮��ĺ�����ϵʽ��
(Ԫ)֮��ĺ�����ϵʽ��
��2�������۵��۶�Ϊ����Ԫʱ�����ľ�ÿ���������������������Ϊ����Ԫ��
��3���̳���Ӫ���������������������![]() ��
��![]() ����Ӫ��������
����Ӫ��������
����![]() �����ľߵ����۵��۸��ڽ��ۣ���������
�����ľߵ����۵��۸��ڽ��ۣ���������![]() Ԫ��
Ԫ��
����![]() ��ÿ��������������
��ÿ��������������![]() ������ÿ���ľߵ���������Ϊ
������ÿ���ľߵ���������Ϊ![]() Ԫ��
Ԫ��
��Ƚ����ַ��������������ߣ���˵�����ɣ�
���𰸡���1��![]() ����2�������۵��۶�Ϊ
����2�������۵��۶�Ϊ![]() Ԫʱ�����ľ�ÿ���������������������Ϊ
Ԫʱ�����ľ�ÿ���������������������Ϊ![]() Ԫ����3��
Ԫ����3��![]() ���������������ߣ����ɼ�������
���������������ߣ����ɼ�������
��������
��1����������=�����۵���-���ۣ������������г�������ϵʽ���ɣ�
��2�����ݣ�1��ʽ�г��ĺ�����ϵʽ�������䷽�������ֵ��
��3���ֱ��������A��B��x��ȡֵ��Χ��Ȼ��ֱ����A��B�������������Ȼ����бȽϣ�
�⣺��1��������ã�������![]() ��
��
��![]()
![]() ��
��
��2��![]() ��
��
![]() ��
��
![]() ����ͼ�����£�
����ͼ�����£�![]() �����ֵ��
�����ֵ��
��![]() ʱ��
ʱ��![]() ��
��
�𣺵����۵��۶�Ϊ![]() Ԫʱ�����ľ�ÿ���������������������Ϊ
Ԫʱ�����ľ�ÿ���������������������Ϊ![]() Ԫ��
Ԫ��
��3��![]() ���������������ߣ��������£�
���������������ߣ��������£�
��![]() ������
������![]() ��
��
![]() ����
����![]() ����ͼ��ĶԳ���Ϊֱ��
����ͼ��ĶԳ���Ϊֱ��![]() ���ҿ������£�
���ҿ������£�
![]() ��
��![]() ʱ��
ʱ��![]() �����ֵ��
�����ֵ��
��ʱ![]() ��
��
��![]() ������
������![]()
��ã�![]() ��
��
![]() ����
����![]() ����ͼ��ĶԳ���Ϊֱ��
����ͼ��ĶԳ���Ϊֱ��![]() ���ҿ������£�
���ҿ������£�
![]() ��
��![]() ʱ��
ʱ��![]() �����ֵ��
�����ֵ��
��ʱ![]() ��
��
![]() ��
��
![]() ���������������ߣ�
���������������ߣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����OABC�Ķ���A������Ϊ(5��0)������B��C���ڵ�һ���ޣ��Խ���AC��BO���ڵ�D��˫����y=![]() ��x��0��������D����ACBO40����k��ֵΪ�� ��
��x��0��������D����ACBO40����k��ֵΪ�� ��
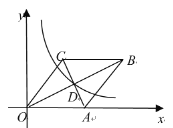
A.6B.8C.10D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯��ѧ��Ȥ̽�������˼����Сʵͬѧ��̽������ֱ�ߵ�λ�ù�ϵ��������ʱ���֣����������ഹֱ�������γ�Ϊ���д�������������ͼ1��ͼ2��ͼ3�У�![]() ��
��![]() ��
��![]() �����ߣ�
�����ߣ�![]() �ڵ�
�ڵ�![]() ����
����![]() �����������ξ���Ϊ���д�����������
�����������ξ���Ϊ���д�����������
������̽����
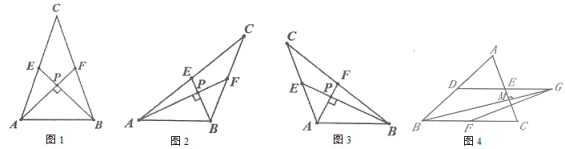
��1����ͼ1����![]() ��
��![]() ʱ��
ʱ��![]() _____��
_____��![]() ______��
______��
��ͼ2����![]() ��
��![]() ʱ��
ʱ��![]() _____��
_____��![]() ______��
______��
������֤����
��2������۲죨1���еļ�����������![]() ��
��![]() ��
��![]() ����֮��Ĺ�ϵ���õ�ʽ��ʾ������������ͼ3֤����Ľ��ۣ�
����֮��Ĺ�ϵ���õ�ʽ��ʾ������������ͼ3֤����Ľ��ۣ�
����չ֤����
��3����ͼ4����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]()
![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() ��ʹ��
��ʹ��![]() ������
������![]() ����
����![]() �ڵ�
�ڵ�![]() ʱ����
ʱ����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ABC��,��ACB=120����BC=4��DΪAB���е㣬DC��BC������ABC�������___.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ӵ�A��һɽ���ϵĵ��߸�PQ���۲��P��������45������ǰ��6m����B�㣬��ö��˵�P�˵˵�Q�����Ƿֱ���60����30������õ��߸�PQ�ĸ߶ȣ�������
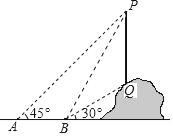
A. 6+2![]() B. 6+
B. 6+![]() C. 10��
C. 10��![]() D. 8+
D. 8+![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() �Ķ���Ϊ��
�Ķ���Ϊ��![]() ����
����![]() ��ĸ����ύ�ڵ�
��ĸ����ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ��������W����һ��
��������W����һ��![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��
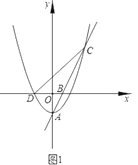
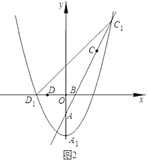
��1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2������![]() ��
��![]() �ᣬ��
�ᣬ��![]() ���ڵ�
���ڵ�![]() ����
����![]() ƽ��
ƽ��![]() ����������W�Ľ���ʽ��
����������W�Ľ���ʽ��
��3����![]() ����������W����ƽ��
����������W����ƽ��![]() ����λ�õ�������
����λ�õ�������![]() ����ͼ2����������
����ͼ2����������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ����
����![]() �Ḻ����Ľ���Ϊ
�Ḻ����Ľ���Ϊ![]() ��������
��������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ���ʣ���ƽ�ƵĹ����У�
���ʣ���ƽ�ƵĹ����У�![]() �Ƿ��Ϊ��ֵ�����ǣ������
�Ƿ��Ϊ��ֵ�����ǣ������![]() ��ֵ�������ǣ���˵�����ɣ�
��ֵ�������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
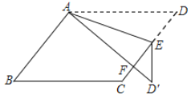
����Ŀ����ͼ����ƽ���ı���![]() �У�
�У�![]() Ϊ��
Ϊ��![]() �ϵ㣬��
�ϵ㣬��![]() ��
��![]() �۵���
�۵���![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ����
����![]() �Ķ���Ϊ_________��
�Ķ���Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
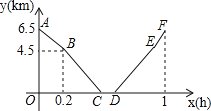
����Ŀ���Ӽص��ҵأ�����һ������·��Ȼ����һ��ƽ·��С���ﳵ�Ӽس����������ҵغ���Ϣһ��ʱ�䣬Ȼ��ԭ·���ؼأ�����С���ﳵ�����¡�ƽ·������ʱ�ֱ𱣳�����ǰ������֪С���ﳵ���µ��ٶȱ�ƽ·�ϵ��ٶ�ÿСʱ��5km�����µ��ٶȱ���ƽ·�ϵ��ٶ�ÿСʱ��5km����С������xh�������ҵ�ykm�ĵط���ͼ�е�����ABCDEF��ʾy��x֮��ĺ�����ϵ��
��1��С���ﳵ��ƽ·�ϵ��ٶ�Ϊ�� ��km/h�������ҵ���Ϣ���� ��h��
��2���ֱ����߶�AB��EF����Ӧ�ĺ�����ϵʽ��
��3���Ӽص��ҵؾ������أ����С�����ξ������ص�ʱ����Ϊ0.85h����������֮���·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
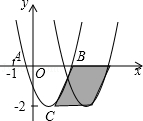
����Ŀ����ͼ����֪������y=ax2+bx+c��x�ύ��A��B���㣬����C��������Ϊ��2���ֽ�����������ƽ��2����λ���õ�������y=a1x2+b1x+c1�������н�����ȷ���� ����д��������ȷ���۵���ţ�
��b��0
��a��b+c��0
����Ӱ���ֵ����Ϊ4
����c=��1����b2=4a��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com