Question

1．在平面直角坐标系xOy中，定义点P（x，y）的变换点为P′（x+y，x-y）．
（1）如图1，如果⊙O的半径为$2\sqrt{2}$，
①请你判断M（2，0），N（-2，-1）两个点的变换点与⊙O的位置关系；
②若点P在直线y=x+2上，点P的变换点P′在⊙O的内，求点P横坐标的取值范围．
（2）如图2，如果⊙O的半径为1，且P的变换点P′在直线y=-2x+6上，求点P与⊙O上任意一点距离的最小值．

Answer 1

分析 （1）①根据新定义得到点M的变换点M′的坐标为（2，2），于是根据勾股定理计算出OM′=2$\sqrt{2}$，则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上；同样方法可判断点N（-2，-1）的变换点在⊙O外
②利用一次函数图象上点的坐标特征，设P点坐标为（x，x+2），利用新定义得到P点的变换点为P′的坐标为（2x+2，-2），则根据勾股定理计算出OP′=$\sqrt{（2x+2）^{2}+（-2）^{2}}$，然后利用点与圆的位置关系得到$\sqrt{（2x+2）^{2}+（-2）^{2}}$＜2$\sqrt{2}$，解不等式得-2＜x＜0；
（2）设点P′的坐标为（x，-2x+6），P（m，n），根据新定义得到m+n=x，m-n=-2x+6，消去x得3m+n=6，则n=-3m+6，于是得到P点坐标为（m，-3m+6），则可判断点P在直线y=-3x+6上，设直线y=-3x+6与x轴相交于点A，与y轴相交于点B，过O点作OH⊥AB于H，交⊙O于C，如图2，易得A（2，0），B（0，6），利用勾股定理计算出AB=2$\sqrt{10}$，再利用面积法计算出OH=$\frac{3\sqrt{10}}{5}$，所以CH=$\frac{3\sqrt{10}}{5}$-1，当点P在H点时，PC为点P与⊙O上任意一点距离的最小值．

解答 解：（1）①M（2，0）的变换点M′的坐标为（2，2），则OM′=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，所以点M（2，0）的变换点在⊙O上；
N（-2，-1）的变换点N′的坐标为（-3，-1），则ON′=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$＞2$\sqrt{2}$，所以点N（-2，-1）的变换点在⊙O外；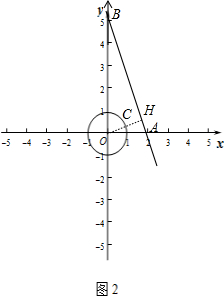
②设P点坐标为（x，x+2），则P点的变换点为P′的坐标为（2x+2，-2），则OP′=$\sqrt{（2x+2）^{2}+（-2）^{2}}$，
∵点P′在⊙O的内，
∴$\sqrt{（2x+2）^{2}+（-2）^{2}}$＜2$\sqrt{2}$，
∴（2x+2）²＜4，即（x+1）²＜1，
∴-1＜x+1＜1，解得-2＜x＜0，
即点P横坐标的取值范围为-2＜x＜0；
（2）设点P′的坐标为（x，-2x+6），P（m，n），
根据题意得m+n=x，m-n=-2x+6，
∴3m+n=6，
即n=-3m+6，
∴P点坐标为（m，-3m+6），
∴点P在直线y=-3x+6上，
设直线y=-3x+6与x轴相交于点A，与y轴相交于点B，过O点作OH⊥AB于H，交⊙O于C，如图2，
则A（2，0），B（0，6），
∴AB=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$，
∵$\frac{1}{2}$OH•AB=$\frac{1}{2}$OA•OB，
∴OH=$\frac{2×6}{2\sqrt{10}}$=$\frac{3\sqrt{10}}{5}$，
∴CH=$\frac{3\sqrt{10}}{5}$-1，
即点P与⊙O上任意一点距离的最小值为$\frac{3\sqrt{10}}{5}$-1．

点评 本题考查了圆的综合题：熟练掌握点与圆的位置关系和一次函数图象上点的坐标特征；会运用勾股定理定理和面积法计算线段的长；提高阅读理解能力．