
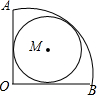
 如图,已知扇形半径是1,圆心角是直角,则扇形内切圆半径是$\frac{1}{2}$.
如图,已知扇形半径是1,圆心角是直角,则扇形内切圆半径是$\frac{1}{2}$. 分析 设OA,OB和圆分别相切于点D,C,连接MD,MC,OM,BM,易证四边形DOCM是正方形,由正方形的性质以及扇形和圆的对称性可得OM=BM,进而可得OC=$\frac{1}{2}$OB,再由等腰直角三角形的性质即可求出MC的长,即扇形内切圆半径的长.
解答 解:设OA,OB和圆分别相切于点D,C,连接MD,MC,OM,BM,
∴OD=OC,∠MDO=∠MCO=90°,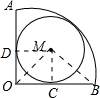
∵∠AOB=90°,
∴四边形DOCM是正方形,
∴∠MOC=45°,
∵MC⊥OB,
∴△OMC是等腰直角三角形,
∵OA=OB,点M为内切圆圆心,
∴AM=BM,
∵OM=$\frac{1}{2}$AB,
∴OM=BM,
∴OC=$\frac{1}{2}$OB=$\frac{1}{2}$,
∴MC=OC=$\frac{1}{2}$,
即扇形内切圆半径的长为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题综合运考查了切线长定理、三角形的内心的性质以及直角三角形的性质和正方形的判定和性质、等腰直角三角形的判定和性质,题目的综合性较强,正确添加图形的辅助线是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,正△ABC与正△A1B1C1关于某点中心对称,已知A,A1,B三点的坐标分别是(0,4),(0,3),(0,2).
如图,正△ABC与正△A1B1C1关于某点中心对称,已知A,A1,B三点的坐标分别是(0,4),(0,3),(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
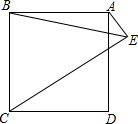 如图,若点E为正方形ABCD外一点,∠BEC=45°,连接AE.
如图,若点E为正方形ABCD外一点,∠BEC=45°,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
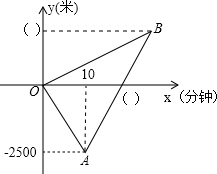 早上小芳和妈妈同时从家里出发,小芳步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是她们离家的距离y(米)与时间x(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小芳的电话,立即以原速度前往学校,若已知小芳步行的速度为50米/分钟,并且妈妈与小芳同时到达学校.
早上小芳和妈妈同时从家里出发,小芳步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是她们离家的距离y(米)与时间x(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小芳的电话,立即以原速度前往学校,若已知小芳步行的速度为50米/分钟,并且妈妈与小芳同时到达学校.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com