
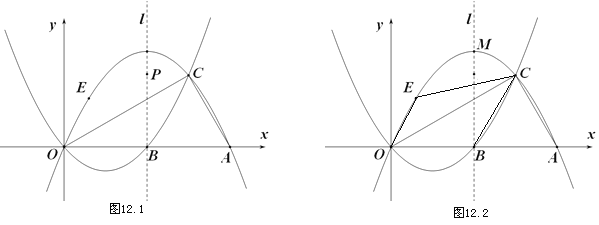
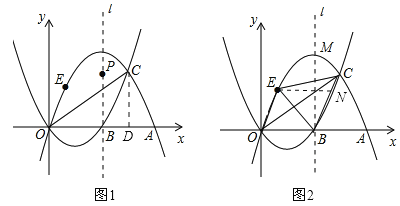
【题目】如图,抛物线![]() :
:![]() 与
与![]() :
:![]() 相交于点
相交于点![]() 、
、![]() ,
,![]() 与
与![]() 分别交
分别交![]() 轴于点
轴于点![]() 、
、![]() ,且
,且![]() 为线段
为线段![]() 的中点.
的中点.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)抛物线![]() 的对称轴为
的对称轴为![]() ,顶点为
,顶点为![]() ,在(2)的条件下:
,在(2)的条件下:
①点![]() 为抛物线
为抛物线![]() 对称轴
对称轴![]() 上一动点,当
上一动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
②如图12.2,点![]() 在抛物线
在抛物线![]() 上点
上点![]() 与点
与点![]() 之间运动,四边形
之间运动,四边形![]() 的面积是否存在最大值?若存在,求出面积的最大值和点
的面积是否存在最大值?若存在,求出面积的最大值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①P(
;(3)①P(![]() ,
,![]() );②存在,
);②存在,![]()
【解析】
(1)由两抛物线解析式可分别用a和b表示出A、B两点的坐标,利用B为OA的中点可得到a和b之间的关系式;
(2)由抛物线解析式可先求得C点坐标,过C作CD⊥x轴于点D,可证得△OCD∽△CAD,由相似三角形的性质可得到关于a的方程,可求得OA和CD的长,可求得△OAC的面积;
(3)①连接OC与l的交点即为满足条件的点P,可求得OC的解析式,则可求得P点坐标;
②设出E点坐标,则可表示出△EOB的面积,过点E作x轴的平行线交直线BC于点N,可先求得BC的解析式,则可表示出EN的长,进一步可表示出△EBC的面积,则可表示出四边形OBCE的面积,利用二次函数的性质可求得其最大值,及E点的坐标.
解:
(1)在y=x2+ax中,
当y=0时,x2+ax=0,x1=0,x2=﹣a,
∴B(﹣a,0),
在y=﹣x2+bx中,
当y=0时,﹣x2+bx=0,x1=0,x2=b,
∴A(0,b),
∵B为OA的中点,
∴b=﹣2a,
∴![]() ;
;
(2)联立两抛物线解析式可得: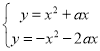 ,
,
消去y整理可得![]() ,
,
解得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
∴C(![]() ,
,![]() ),
),
过C作CD⊥x轴于点D,如图1,
∴D(![]() ,0),
,0),
∵∠OCA=90°,
∴△OCD∽△CAD,
∴![]() ,
,
∴CD2=ADOD,即![]() ,
,
∴a1=0(舍去),![]() (舍去),
(舍去),![]() ,
,
∴OA=-2a=![]() ,CD=
,CD=![]() =1,
=1,
∴![]() ;
;
(3)①抛物线![]() ,
,
∴其对称轴![]() ,点A关于l2的对称点为O(0,0),C(
,点A关于l2的对称点为O(0,0),C(![]() ,1),
,1),
则P为直线OC与l2的交点,
设OC的解析式为y=kx,
∴1=![]() k,得k=
k,得k=![]() ,
,
∴OC的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴P(![]() ,
,![]() );
);
②设E(m,![]() )(
)(![]() ),则
),则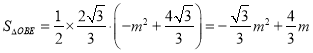 ,
,
而B(![]() ,0),C(
,0),C(![]() ,1),
,1),
设直线BC的解析式为y=kx+b,
由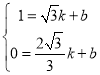 ,解得:k=
,解得:k=![]() ,b=-2,
,b=-2,
∴直线BC的解析式为![]() ,
,
过点E作x轴的平行线交直线BC于点N,如图2,
则![]() ,即x=
,即x=![]()
∴EN=![]()
∴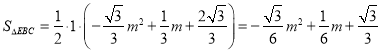
∴S四边形OBCE=S△OBE+S△EBC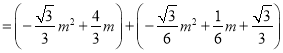
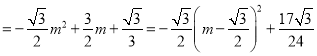 ,
,
![]() ,
,
∴当![]() 时,
时,![]() ,
,
当![]() 时,
时,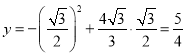 ,
,
∴E(![]() ,
,![]() ),
),![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,FD切
,FD切![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
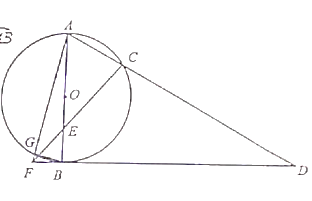
(1)求证:![]() ;
;
(2)若![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
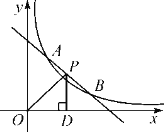
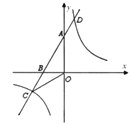
【题目】如图,一次函数y=-x+b与反比例函数y=![]() (x>0)的图象交于点A(m,3)和B(3,1).
(x>0)的图象交于点A(m,3)和B(3,1).
(1)求一次函数和反比例函数的解析式;
(2)点P(x,y)是直线AB上在第一象限内的一个点,过点P作PD⊥x轴于点D,连接OP,令△POD的面积为S,当S>![]() 时,直接写出点P横坐标x的取值范围.
时,直接写出点P横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=10,AC是⊙O的弦.过点C作⊙O的切线DE交AB的延长线于点E,过点A作AD⊥DE,垂足为D,与⊙O交于点F,设∠DAC、∠CEA的度数分别为α,β,且0°<α<45°
(1)用含α的代数式表示β;
(2)连结OF交AC于点G,若AG=CG,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】收发微信红包已成为各类人群进行交流联系,增强感情的一部分,下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.
请问:(1)2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少?
(2)2017年六一甜甜和她妹妹各收到了多少钱的微信红包?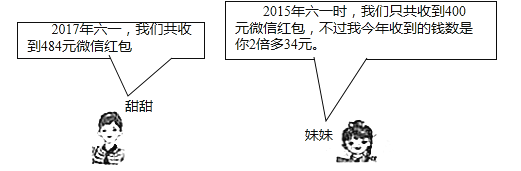
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,若 P是口ABCD 边 CD 上任意一点,连结 AP、BP,若△APB 的面积为 60 ,△APD 的面积为 18,则 S△APC= .
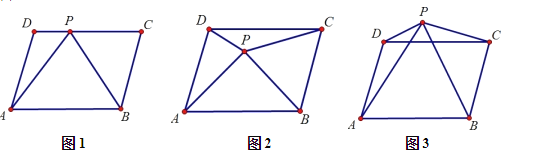
(2) 如图 2,①若点 P 运动到口ABCD 内一点时,试说明 S△APB +S△DPC =S△BPC +S△APD.
②若此时△APB 的面积为 60,△APD 的面积为 18,则 S△APC= .
(3)如图 3①利用(2)中的方法你会发现,S△APB ,S△DPC ,S△BPC ,S△APD 之间存在怎样的关系: .
②若此时△APB 的面积为 60,△APD 的面积为 18,请利用你的发现,求 S△APC 的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,直线
,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 和点
和点![]() .
.
(1)求直线![]() 与反比例函数的解析式;
与反比例函数的解析式;
(2)求![]() 的度数;
的度数;
(3)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角(
角(![]() 为锐角),得到
为锐角),得到![]() ,当
,当![]() 为多少度时
为多少度时![]() ,并求此时线段
,并求此时线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,其部分图象如图所示,有下列结论:①
,其部分图象如图所示,有下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 增大而增大;④抛物线的顶点坐标为
增大而增大;④抛物线的顶点坐标为![]() ;⑤若方程
;⑤若方程![]() 两根为
两根为![]() (
(![]() ),则
),则![]() ,
,![]() .其中正确结论有( )
.其中正确结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
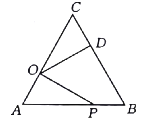
【题目】如图,在等边![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 是
是![]() 上一动点,连接
上一动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,若要使点
,若要使点![]() 恰好在
恰好在![]() 上,则
上,则![]() 的长为().
的长为().
A. 4B. 5C. 6D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com