
【题目】如图,已知⊙O的直径AB=10,AC是⊙O的弦.过点C作⊙O的切线DE交AB的延长线于点E,过点A作AD⊥DE,垂足为D,与⊙O交于点F,设∠DAC、∠CEA的度数分别为α,β,且0°<α<45°
(1)用含α的代数式表示β;
(2)连结OF交AC于点G,若AG=CG,求AC的长.

【答案】(1)β=90°﹣2α;(2)AC=5![]()
【解析】
(1)连接OC,根据切线的性质得到OC⊥DE,得到OC∥AD,根据平行线的性质、圆周角定理计算即可;
(2)证明△AGF≌△AGO,根据全等三角形的性质得到OG=GF,根据勾股定理求出AG,根据垂径定理解答即可.
解:(1)连接OC,
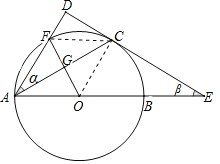
∵CE是⊙O的切线,
∴OC⊥DE,又AD⊥DE,
∴OC∥AD,
∴∠ACO=α,
∵OA=OC,
∴∠OAC=∠ACO=α,
∴∠EOC=2α,
∴β=90°﹣2α;
(2)在△AGF和△AGO中,
 ,
,
∴△AGF≌△AGO(ASA)
∴OG=GF,
∴OG=![]() OA=
OA=![]() ,
,
由勾股定理得,AG=![]() ,
,
∵OF⊥AC,
∴AC=2AG=![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
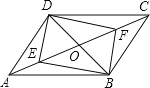
A.∠ADE=∠CBFB.∠ABE=∠CDFC.DE=BFD.OE=OF
查看答案和解析>>
科目:初中数学 来源: 题型:
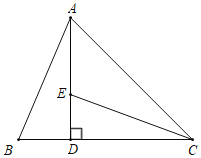
【题目】如图,在△ABC中,∠ACB=45°,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.
(1)求证:△ABD≌△CED;
(2)若CE为∠ACD的角平分线,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
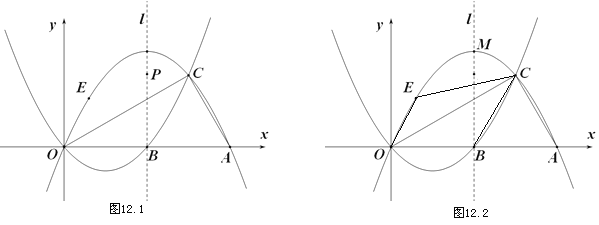
【题目】如图,抛物线![]() :
:![]() 与
与![]() :
:![]() 相交于点
相交于点![]() 、
、![]() ,
,![]() 与
与![]() 分别交
分别交![]() 轴于点
轴于点![]() 、
、![]() ,且
,且![]() 为线段
为线段![]() 的中点.
的中点.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)抛物线![]() 的对称轴为
的对称轴为![]() ,顶点为
,顶点为![]() ,在(2)的条件下:
,在(2)的条件下:
①点![]() 为抛物线
为抛物线![]() 对称轴
对称轴![]() 上一动点,当
上一动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
②如图12.2,点![]() 在抛物线
在抛物线![]() 上点
上点![]() 与点
与点![]() 之间运动,四边形
之间运动,四边形![]() 的面积是否存在最大值?若存在,求出面积的最大值和点
的面积是否存在最大值?若存在,求出面积的最大值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l切⊙O于点A,B为⊙O上一点,过点B作BC⊥l,垂足为点C,连接AB、OB.
(1)求证:∠ABC=∠ABO;
(2)若AB=![]() ,AC=1,求⊙O的半径.
,AC=1,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某校九年级学生为灾区捐款情况抽样调查的条形图和扇形统计图.
(1)求抽样调查的人数;
(2)在扇形统计图中,求该样本中捐款15元的人数所占的圆心角度数;
(3)若该校九年级学生有1000人,据此样本估计九年级捐款总数为多少元?
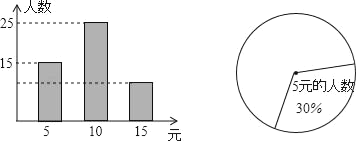
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com