
���� ��1������������������˳������㷨����㣬Ȼ��Ƚϴ�С���ɣ�
��2�����������ȽϽ���ܽ�����еĹ��ɣ�
��� �⣺��1���١�42+52=16+25=41��2��4��5=40��
��42+52��2��4��5��
�ڡߣ�-1��2+22=1+4=5��2����-1����2=-4��
�ࣨ-1��2+22��2����-1����2��
�ۡ�32+��$\frac{1}{3}$��2=9+$\frac{1}{9}$=9$9\frac{1}{9}$��2��3��$\frac{1}{3}$=2��
��32+��$\frac{1}{3}$��2��2��3��$\frac{1}{3}$��
�ܡ�32+32=9+9=18��2��3��3=18��
��32+32=2��3��3��
�ʴ�Ϊ���٣����ڣ����ۣ�����=��
��2���ɣ�1����֪����a��bʱ��a2+b2��2ab����a=bʱ��a2+b2=2ab��
���� ������Ҫ������������ʽ��ֵ�������������㡢�Ƚ��������Ĵ�С������������������˳������㷨���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
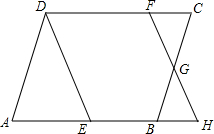 ��ͼ��E��ƽ���ı��ε�AB����һ�㣬����DE����FH��DE���ֱ�CD��BC��AB���ӳ����ڵ�F��G��H����֤����ADE�ס�CGH��
��ͼ��E��ƽ���ı��ε�AB����һ�㣬����DE����FH��DE���ֱ�CD��BC��AB���ӳ����ڵ�F��G��H����֤����ADE�ס�CGH���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
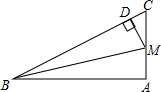 ��ABC�У���A=90�㣬MΪAC���е㣬MD��BC��DΪ���㣬˵����BD2-CD2=AB2��
��ABC�У���A=90�㣬MΪAC���е㣬MD��BC��DΪ���㣬˵����BD2-CD2=AB2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x+3 | B�� | y=2x-3 | C�� | y=3x-3 | D�� | y=4x-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com