
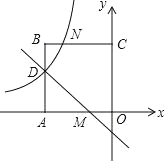
【题目】(2016山东省泰安市第25题)如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
【答案】(1)、y=-x-1;(2)、(﹣10,9)或(8,﹣9)
【解析】
试题分析:(1)、由正方形OABC的顶点C坐标,确定出边长,及四个角为直角,根据AD=2DB,求出AD的长,确定出D坐标,代入反比例解析式求出m的值,再由AM=2MO,确定出MO的长,即M坐标,将M与D坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;(2)、把y=3代入反比例解析式求出x的值,确定出N坐标,得到NC的长,设P(x,y),根据△OPM的面积与四边形OMNC的面积相等,求出y的值,进而得到x的值,确定出P坐标即可.
试题解析:(1)、∵正方形OABC的顶点C(0,3),∴OA=AB=BC=OC=3,∠OAB=∠B=∠BCO=90°,
∵AD=2DB, ∴AD=![]() AB=2, ∴D(﹣3,2), 把D坐标代入y=
AB=2, ∴D(﹣3,2), 把D坐标代入y=![]() 得:m=﹣6,
得:m=﹣6,
∴反比例解析式为y=﹣![]() , ∵AM=2MO,∴MO=
, ∵AM=2MO,∴MO=![]() OA=1,即M(﹣1,0),
OA=1,即M(﹣1,0),
把M与D坐标代入y=kx+b中得:![]() ,解得:k=b=﹣1,则直线DM解析式为y=﹣x﹣1;
,解得:k=b=﹣1,则直线DM解析式为y=﹣x﹣1;
(2)、把y=3代入y=﹣![]() 得:x=﹣2,∴N(﹣2,3),即NC=2,
得:x=﹣2,∴N(﹣2,3),即NC=2,
设P(x,y), ∵△OPM的面积与四边形OMNC的面积相等,
∴![]() (OM+NC)OC=
(OM+NC)OC=![]() OM|y|,即|y|=9, 解得:y=±9,
OM|y|,即|y|=9, 解得:y=±9,
当y=9时,x=﹣10,当y=﹣9时,x=8,则P坐标为(﹣10,9)或(8,﹣9).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】有足够多的长方形和正方形卡片,如图.


(1)如图,如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙).请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.
这个长方形的代数意义是______________;
(2)小明想用类似方法解释多项式乘法![]() .
.
那么需用2号卡片_________张,3号卡片_____________张.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两千多年前,古希腊数学家欧几里得首次运用某种数学思想整理了几何知识,完成 了数学著作《原本》,欧几里得首次运用的这种数学思想是( )
A.公理化思想B.数形结合思想C.抽象思想D.模型思想
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com