
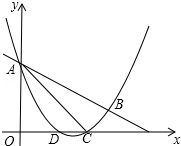
 ��ͼ��������y=$\frac{1}{2}$x2+mx+n��ֱ��y=-$\frac{1}{2}$x+3����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����C��3��0����
��ͼ��������y=$\frac{1}{2}$x2+mx+n��ֱ��y=-$\frac{1}{2}$x+3����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����C��3��0�������� ����ֻ���A��C������������y=$\frac{1}{2}$x2+mx+n���Ϳɵõ������ߵĽ���ʽ��Ȼ�����ֱ��AB�������ߵĽ���B�����꣬����B��BH��x����H����ͼ1���á�BCH=��ACO=45�㣬BC=$\sqrt{2}$��AC=3$\sqrt{2}$���Ӷ��õ���ACB=90�㣬Ȼ��������Ǻ����Ķ���Ϳ����tan��BAC��ֵ��
������P��PG��y����G�����PGA=90�㣮���P�ĺ�����Ϊx����P��y���Ҳ�ɵ�x��0����PG=x���á�APQ=��ACB=90�㣮����G�ڵ�A���·����ٵ���PAQ=��CABʱ����PAQ�ס�CAB����ʱ��֤�á�PGA�ס�BCA���������������ε����ʿɵ�AG=3PG=3x������P��x��3-3x����Ȼ���P��x��3-3x�����������ߵĽ���ʽ���Ϳ������P������ڵ���PAQ=��CBAʱ����PAQ�ס�CBA��ͬ�����������P�����ꣻ����G�ڵ�A���Ϸ���ͬ�����������P�����ꣻ
��� 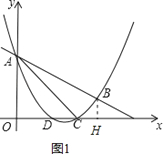 �⣺����A��0��3����C��3��0������y=$\frac{1}{2}$x2+mx+n����
�⣺����A��0��3����C��3��0������y=$\frac{1}{2}$x2+mx+n����
$\left\{\begin{array}{l}{n=3}\\{\frac{1}{2}��9+mx+n=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=-\frac{5}{2}}\\{n=3}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{2}$x2-$\frac{5}{2}$x+3��
����$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=\frac{1}{2}{x}^{2}-\frac{5}{2}x+3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$��$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$��
���B��������4��1����
����B��BH��x����H����ͼ1����C��3��0����B��4��1����
��BH=1��OC=3��OH=4��CH=4-3=1����BH=CH=1��
�ߡ�BHC=90�㣬���BCH=45�㣬BC=$\sqrt{2}$��
ͬ������ACO=45�㣬AC=3$\sqrt{2}$��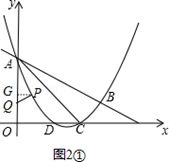
���ACB=180��-45��-45��=90�㣬
��tan��BAC=$\frac{BC}{AC}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$��
����1�����ڵ�P��ʹ����A��P��QΪ��������������ACB���ƣ�
����P��PG��y����G�����PGA=90�㣮
���P�ĺ�����Ϊx����P��y���Ҳ�ɵ�x��0����PG=x��
��PQ��PA����ACB=90�㣬���APQ=��ACB=90�㣮
����G�ڵ�A���·���
����ͼ2�٣�����PAQ=��CABʱ�����PAQ�ס�CAB��
�ߡ�PGA=��ACB=90�㣬��PAQ=��CAB�����PGA�ס�BCA��
��$\frac{PG}{AG}$=$\frac{BC}{AC}$=$\frac{1}{3}$��
��AG=3PG=3x��
��P��x��3-3x������P��x��3-3x������y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3���ã�$\frac{1}{2}$x2-$\frac{5}{2}$x+3=3-3x��
�����ã�x2+x=0����ã�x1=0����ȥ����x2=-1����ȥ����
����ͼ2�ڣ�����PAQ=��CBAʱ�����PAQ�ס�CBA��
ͬ���ɵã�AG=$\frac{1}{3}$PG=$\frac{1}{3}$x����P��x��3-$\frac{1}{3}$x����
��P��x��3-$\frac{1}{3}$x������y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3���ã�$\frac{1}{2}$x2-$\frac{5}{2}$x+3=3-$\frac{1}{3}$x��
�����ã�x2-$\frac{13}{3}$x=0����ã�x1=0����ȥ����x2=$\frac{13}{3}$����P��$\frac{13}{3}$��$\frac{14}{9}$����
����G�ڵ�A���Ϸ���
�ٵ���PAQ=��CABʱ�����PAQ�ס�CAB��
ͬ���ɵã���P������Ϊ��11��36����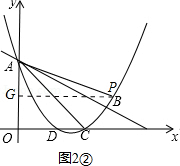
�ڵ���PAQ=��CBAʱ�����PAQ�ס�CBA��
ͬ���ɵã���P������ΪP��$\frac{17}{3}$��$\frac{44}{9}$����
�������������������ĵ�P������Ϊ��11��36������$\frac{13}{3}$��$\frac{14}{9}$������$\frac{17}{3}$��$\frac{44}{9}$����
���� ������Ҫ���������ô���ϵ�����������ߵĽ���ʽ����ֱ���������ߵĽ������ꡢ�������ϵ���������������Ǻ����Ķ��塢���������ε��ж������ʡ���һԪ���η��̡�����֮���߶���̡���ԳƵ����ʡ����ε��ж������ʡ����ɶ�����֪ʶ���ۺ���ǿ���Ѷȴ�


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
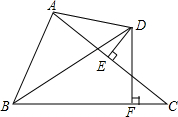 ��ͼ����ABC�У�AC�Ĵ�ֱƽ����DE��AC��E������ABC��ƽ������D��DF��BC��F
��ͼ����ABC�У�AC�Ĵ�ֱƽ����DE��AC��E������ABC��ƽ������D��DF��BC��F�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
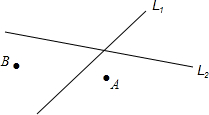 ��ͼ��ֱ��L1��L2��ʾ�����ཻ�Ĺ�·����A��B��ʾ����С������Ҫ�����Ǹ�����һ������վ��ʹ����վ��������·�ľ�����ȣ���������С��ľ���Ҳ��ȣ�����վӦ���ںδ���������ͼ�ϱ������վ��λ�ã����ó߹���ͼ����������ͼ�ۼ���
��ͼ��ֱ��L1��L2��ʾ�����ཻ�Ĺ�·����A��B��ʾ����С������Ҫ�����Ǹ�����һ������վ��ʹ����վ��������·�ľ�����ȣ���������С��ľ���Ҳ��ȣ�����վӦ���ںδ���������ͼ�ϱ������վ��λ�ã����ó߹���ͼ����������ͼ�ۼ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
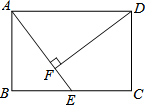 ��ͼ���ھ���ABCD�У�E��BC�ߵ��е㣬DF��AE������ΪF��
��ͼ���ھ���ABCD�У�E��BC�ߵ��е㣬DF��AE������ΪF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
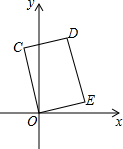 ��ͼ���ھ���COED�У���D�������ǣ�1��3������CE�ij��ǣ�������
��ͼ���ھ���COED�У���D�������ǣ�1��3������CE�ij��ǣ�������| A�� | 3 | B�� | $2\sqrt{2}$ | C�� | $\sqrt{10}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
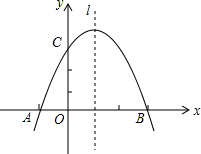 ��֪����ͼ�����κ�����ͼ������y=-x2����ƽ��1����λ��������ƽ��4����λ���õ���
��֪����ͼ�����κ�����ͼ������y=-x2����ƽ��1����λ��������ƽ��4����λ���õ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
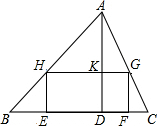 ��ͼ����ABC�У�BC=24cm����AD=12cm������EFGH����������E��F��BC�ϣ�����������G��H�ֱ���AC��AB�ϣ���EF��EH=4��3�����ı���EFGH�������
��ͼ����ABC�У�BC=24cm����AD=12cm������EFGH����������E��F��BC�ϣ�����������G��H�ֱ���AC��AB�ϣ���EF��EH=4��3�����ı���EFGH��������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com