
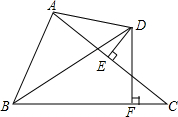
 如图,△ABC中,AC的垂直平分线DE交AC于E,交∠ABC的平分线于D,DF⊥BC于F
如图,△ABC中,AC的垂直平分线DE交AC于E,交∠ABC的平分线于D,DF⊥BC于F分析 (1)①作DH⊥BA交BA的延长线于H,连接DC,根据角平分线的性质得到DF=DH,由DE垂直平分AC,得到AD=CD,推出Rt△ADH≌Rt△CDF,根据全等三角形的性质得到AH=CF,BH=BF,根据线段的和差即可得到结论;②同理BC+BA=BF+CF+BA=BF+AH+BA=BF+BH=2BF;
(2)根据角平分线的性质得到∠DBH=∠DBF=30°,根据三角形的内角和得到∠BDH=∠BDF=60°,求得∠HDF=120°,由于∠HDA=∠FDC,于是得到∠ADC=∠ADF+∠FDC=∠ADF+∠HDA=120°,根据等腰三角形的性质得到∠DAE=∠DCE=30°即可得到结论;
(3)由(2)知:∠ADC=∠HDF=180°-α,于是得到∠DAE=$\frac{1}{2}$[180°-(180°-α)]=$\frac{1}{2}$α.
解答 (1)证明:①作DH⊥BA交BA的延长线于H,连接DC,
∵DB平分∠ABC,
∴DF=DH,
∵DE垂直平分AC,∴AD=CD,
在Rt△ADH与Rt△CDF中,$\left\{\begin{array}{l}{DH=DF}\\{AD=CD}\end{array}\right.$,
∴Rt△ADH≌Rt△CDF,
∴AH=CF,
在Rt△BDH与Rt△BFD中,$\left\{\begin{array}{l}{DH=DF}\\{BD=BD}\end{array}\right.$,
∴Rt△BDH≌Rt△BFD,
∴BH=BF,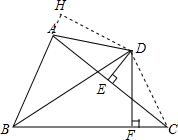 ∴BC-BA=BF+CF-(BH-HA)=BF-BH+2CF=2CF;
∴BC-BA=BF+CF-(BH-HA)=BF-BH+2CF=2CF;
②同理BC+BA=BF+CF+BA=BF+AH+BA=BF+BH=2BF;
(2)证明:∵∠ABC=60°,
∴∠DBH=∠DBF=30°,∴∠BDH=∠BDF=60°,
∴∠HDF=120°,∵∠HDA=∠FDC,
∴∠ADC=∠ADF+∠FDC=∠ADF+∠HDA=120°,∵DA=DC,∴∠DAE=∠DCE=30°,∴∠ADE=60°;
(3)由(2)知:∠ADC=∠HDF=180°-α,
∴∠DAE=$\frac{1}{2}$[180°-(180°-α)]=$\frac{1}{2}$α.
点评 本题考查了全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质,等腰三角形的性质,正确的作出辅助线是解题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
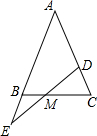 在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.
在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
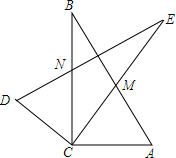 两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.
两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
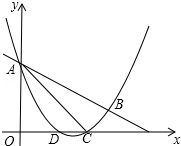 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com