
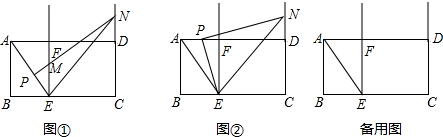
分析 (1)根据线段的垂直平分线的性质,AE=EC,设BE=x,则AE=EC=8-x,在直角△ABE中利用勾股定理即可列方程求得x的值,进而求得AE的长;
(2)分成P在线段AE上和在AD上两种情况进行讨论,利用相似三角形的性质求得ND的长,然后利用三角形的面积公式求解;
(3)利用相似三角形的性质以及勾股定理利用x表示出NE、CM以及CN的长,然后分成三种情况进行讨论,解方程求解.
解答 解:(1)设BE=x,则BE=BC-BE=8-x,
∵E在AC的垂直平分线上,
∴AE=EC=8-x,
在直角△ABE中,AB2+BE2=AE2,则42+x2=(8-x)2,
解得:x=3,
则AE=8-x=8-3=5;
(2)当P在AE上时,即0≤x≤5时,PE=x.
如图①,作PG⊥BC于点G,作PH⊥CD于点H. ∵PG⊥BC,∠B=90°,
∵PG⊥BC,∠B=90°,
∴△PGE∽△ABE,
∴$\frac{GE}{BE}=\frac{PG}{AB}=\frac{PE}{AE}$,则$\frac{GE}{3}=\frac{PG}{4}=\frac{x}{5}$,
∴GE=$\frac{3}{5}$x,PG=$\frac{4}{5}$x.
∵∠NPE=∠HPG,
∴∠NPH=∠GPE,
又∵∠PGE=∠NHP=90°,
∴△PHN∽△PGE,
∴△PHN∽△ABE,
∴$\frac{PH}{AB}=\frac{HN}{BE}$,即$\frac{5+\frac{3}{5}x}{4}=\frac{HN}{3}$,
∴HN=$\frac{9}{20}x+\frac{15}{4}$,
∴DN=HN+CH-CD=$\frac{9}{20}x$+$\frac{15}{4}$+$\frac{4}{5}$x-4=$\frac{5}{4}$x-$\frac{1}{4}$,
则S=$\frac{1}{2}$DN•EC=$\frac{1}{2}$×($\frac{5}{4}$x-$\frac{1}{4}$)×5,即S=$\frac{25}{8}$x-$\frac{5}{8}$;
当P在AD上时,即5<t≤13时,作PK⊥BC与点K.
同理可得△PEF∽△NPD,
则$\frac{ND}{PF}=\frac{PD}{EF}$,即$\frac{ND}{3-(x-5)}=\frac{8-(x-5)}{4}$,
解得:DN=$\frac{(8-x)(13-x)}{4}$,
则S=$\frac{1}{2}$×5×$\frac{(8-x)(13-x)}{4}$,即S=$\frac{5(8-x)(13-x)}{4}$;
(3)设EF交PH于点R,则△PMR∽△ABE,
则$\frac{MR}{BE}=\frac{PR}{AB}$,$\frac{PR}{3}=\frac{\frac{3}{5}x}{4}$,
解得:PR=$\frac{9}{20}$x,则EM=$\frac{4}{5}$x+$\frac{9}{20}x$=$\frac{5}{4}$x,
当CM=NM时,EM=$\frac{1}{2}$CN,即$\frac{5}{4}$x=$\frac{1}{2}$×($\frac{9}{20}x+\frac{15}{4}$+$\frac{4}{5}$x),
解得:x=3;
当CM=CN时,CM2=EC2+EM2,则CM2=25+($\frac{5}{4}$x)2=25+$\frac{25}{16}{x}^{2}$,
则25+$\frac{25}{16}$x2=($\frac{9}{20}x+\frac{15}{4}$+$\frac{4}{5}$x)2,解得:x=$\frac{7}{6}$;
当NM=CN时,NM2=EC2+(NC-ME)2=25+($\frac{9}{20}$x+$\frac{15}{4}$+$\frac{4}{5}$x-$\frac{5}{4}$x)2=25+$\frac{225}{16}$,则MN=$\frac{15}{4}$,
则$\frac{9}{20}$x+$\frac{15}{4}$+$\frac{4}{5}$x=$\frac{15}{4}$,解得:x=0.
点评 本题考查了相似三角形的判定与性质,以及订勾股定理的应用,正确利用x表示出EM,CN以及DN的长是关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:解答题
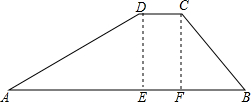 如图,水库大坝的横截面是梯形,坝顶CD宽是5m,坝高DE为20m,斜坡AD的坡度为1:$\sqrt{3}$,斜坡CB的坡度为5:6,建造这样的大坝1000m需要多少m3的土?(结果保留根号)
如图,水库大坝的横截面是梯形,坝顶CD宽是5m,坝高DE为20m,斜坡AD的坡度为1:$\sqrt{3}$,斜坡CB的坡度为5:6,建造这样的大坝1000m需要多少m3的土?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
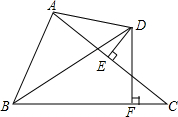 如图,△ABC中,AC的垂直平分线DE交AC于E,交∠ABC的平分线于D,DF⊥BC于F
如图,△ABC中,AC的垂直平分线DE交AC于E,交∠ABC的平分线于D,DF⊥BC于F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
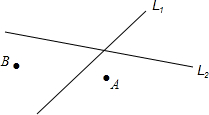 如图,直线L1、L2表示两条相交的公路,点A,B表示两个小镇,现在要在它们附近建一个加油站,使加油站到两条公路的距离相等,并到两个小镇的距离也相等,加油站应建在何处?请你在图上标出加油站的位置.(用尺规作图,并保留作图痕迹)
如图,直线L1、L2表示两条相交的公路,点A,B表示两个小镇,现在要在它们附近建一个加油站,使加油站到两条公路的距离相等,并到两个小镇的距离也相等,加油站应建在何处?请你在图上标出加油站的位置.(用尺规作图,并保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
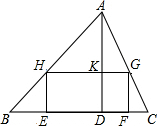 如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求四边形EFGH的面积.
如图,△ABC中,BC=24cm,高AD=12cm,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,且EF:EH=4:3,求四边形EFGH的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com