
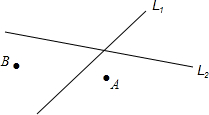
 如图,直线L1、L2表示两条相交的公路,点A,B表示两个小镇,现在要在它们附近建一个加油站,使加油站到两条公路的距离相等,并到两个小镇的距离也相等,加油站应建在何处?请你在图上标出加油站的位置.(用尺规作图,并保留作图痕迹)
如图,直线L1、L2表示两条相交的公路,点A,B表示两个小镇,现在要在它们附近建一个加油站,使加油站到两条公路的距离相等,并到两个小镇的距离也相等,加油站应建在何处?请你在图上标出加油站的位置.(用尺规作图,并保留作图痕迹)  导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 近似数2.50精确到百分位 | B. | 1.45×105精确到千位 | ||
| C. | 近似数13.6亿精确到千万位 | D. | 近似数7000万精确到个位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
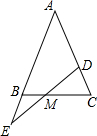 在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.
在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
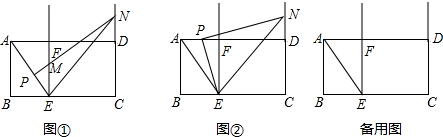
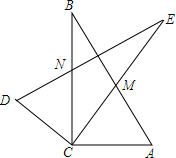 两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.
两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
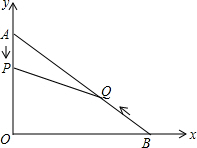 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
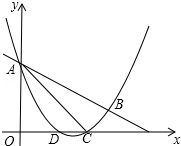 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
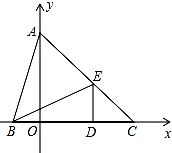 如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com