
 如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41) 分析 过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,设高度为x米,在Rt△AEC中可得CE=$\frac{AE}{tan60°}$=$\frac{\sqrt{3}}{3}x$,在Rt△BFD中有DF=$\frac{BF}{tan45°}$=x,根据AB=EF=CD+DF-CE列出方程,解方程可求得x的值.
解答 解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,
设高度为x米
∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=x米,CD=500米.
在Rt△AEC中,∠C=60°,
∴CE=$\frac{AE}{tan60°}$=$\frac{\sqrt{3}}{3}x$(米).
在Rt△BFD中,∠BDF=45°,
∴DF=$\frac{BF}{tan45°}$=x(米).
∴AB=EF=CD+DF-CE,即500+x-$\frac{\sqrt{3}}{3}$x=541.91
解得:x=99
答:飞机行飞行的高度是99米.
点评 此题考查了俯角的定义、解直角三角形与矩形的性质.注意能借助俯角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
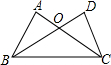 如图,△ABC和△DCB中,∠A=∠D=90°,边AC与DB相交于点O,要使△ABC≌△DCB,则需要添加的一个条件是AB=DC.(写出一种情况即可)
如图,△ABC和△DCB中,∠A=∠D=90°,边AC与DB相交于点O,要使△ABC≌△DCB,则需要添加的一个条件是AB=DC.(写出一种情况即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com