
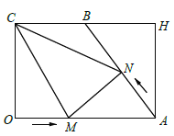
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() . 动点
. 动点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 运动,两个动点同时出发,速度都是每秒1个单位长度,连接
运动,两个动点同时出发,速度都是每秒1个单位长度,连接![]() ,设运动时间为
,设运动时间为![]() (秒)
(秒)![]() . 则
. 则![]() _____时,
_____时,![]() 为直角三角形
为直角三角形
【答案】![]() 或
或![]()
【解析】
△CMN是直角三角形时,有三种情况,一是∠CMN=90°,二是∠MNC=90°,三是∠MCN=90°,然后进行分类讨论求出t的值.
解:
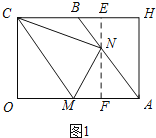
过点N作OA的垂线,交OA于点F,交CH于点E,如图1,
∵B点是CH的中点,
∴BH=![]() CH=
CH=![]() OA=6,
OA=6,
∵AH=OC=8,
∴由勾股定理可求:AB=10,
∵AN=t,
∴BN=10-t,
∵NE∥AH,
∴△BEN∽△BHA,
∴![]() ,
,
∴![]() ,
,
∴EN=![]()
∴FN=8-EN=![]() ,
,
当∠CMN=90°,
由勾股定理可求:AF=![]() ,
,
∵OM=t,
∴AM=12-t,
∴MF=AM-AF=12-t- ![]() =12-
=12-![]() ,
,
∵∠OCM+∠CMO=90°,∠CMO+∠FMN=90°,
∴∠OCM=∠FMN,
∵∠O=∠NFM=90°,
∴△COM∽△MFN,
∴![]() ,
,
∴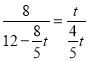 ,
,
∴t=![]() ,
,
当∠MNC=90°,
FN=![]()
∴EN=![]()
∵MF=12-![]()
∴CE=OF=OM+MF=12-![]()
∵∠MNF+∠CNE=90°,
∠ECN+∠CNE=90°,
∴∠MNF=∠ECN,
∵∠CEN=∠NFM=90°,
∴△CEN∽△NFM,
∴![]() ,
,
∴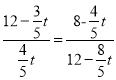 ,
,
∴![]() ,
,
∵0<t<5,
∴![]() ;
;
当∠NCM=90°,
由题意知:此情况不存在,
综上所述,△CMN为直角三角形时,t=![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
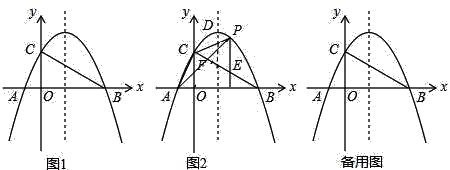
【题目】如图1,抛物线y=ax2+bx+c经过A(﹣2,0)、B(8,0)、C(0,4)三点,顶点为D,连结AC,BC.
(1)求抛物线的函数表达式及顶点D的坐标;
(2)判断三角形ABC的形状,并说明理由;
(3)如图2,点P是该抛物线在第一象限内上的一点.
①过点P作y轴的平行线交BC于点E,若CP=CE,求点P的坐标;
②连结AP交BC于点F,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,A是反比例函数y=![]() (x>0)图象上一点,B是y轴正半轴上一点,以OA,AB为邻边作ABCO.若点C及BC中点D都在反比例函数y=
(x>0)图象上一点,B是y轴正半轴上一点,以OA,AB为邻边作ABCO.若点C及BC中点D都在反比例函数y=![]() (k<0,x<0)图象上,则k的值为( )
(k<0,x<0)图象上,则k的值为( )
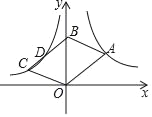
A. ﹣3B. ﹣4C. ﹣6D. ﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:
①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个.
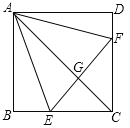
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
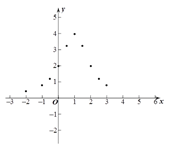
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m﹣3=0.
(1)若该方程的一个根为2,求m的值及方程的另一个根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
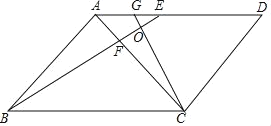
【题目】如图,ABCD中,∠BAC=90°,AB=AC,点E是边AD上一点,且BE=BC,BE交AC于点F,过点C作BE的垂线,垂足为点O,与AD交于点G.
(1)若AB=![]() ,求AE的长;
,求AE的长;
(2)求证;BF=CO+![]() EO.
EO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com