
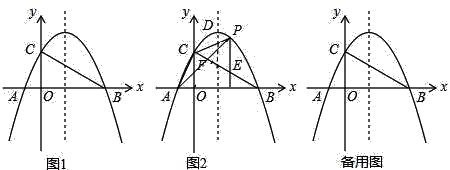
【题目】如图1,抛物线y=ax2+bx+c经过A(﹣2,0)、B(8,0)、C(0,4)三点,顶点为D,连结AC,BC.
(1)求抛物线的函数表达式及顶点D的坐标;
(2)判断三角形ABC的形状,并说明理由;
(3)如图2,点P是该抛物线在第一象限内上的一点.
①过点P作y轴的平行线交BC于点E,若CP=CE,求点P的坐标;
②连结AP交BC于点F,求![]() 的最大值.
的最大值.
【答案】(1)y=![]() x2+
x2+![]() x+4,顶点D坐标为(3,
x+4,顶点D坐标为(3,![]() );(2)三角形ABC是直角三角形,理由详见解析;(3)①P(4,6);②
);(2)三角形ABC是直角三角形,理由详见解析;(3)①P(4,6);②![]() .
.
【解析】
(1)设抛物线的解析式为y=a(x+2)(x-8),将点C的坐标代入可求得a的值,从而得到抛物线的解析式,然后依据抛物线的对称性得到抛物线的对称轴方程,将x=3代入可求得抛物线的顶点坐标.
(2)根据三角形ABC是直角三角形,求得AC2+BC2=AB2,即可利用勾股定理进行证明.
(3)①如图1所示:作CM⊥PE,垂足为M.先利用待定系数法求得BC的解析式,
设点P(m,﹣ ![]() m2+
m2+![]() m+4),则点E(m,﹣
m+4),则点E(m,﹣![]() m+4)﹐M(m,4),接下来依据等腰三角形的性质可得到PM=EM,从而得到关于m的方程,于是可求得点P的坐标.
m+4)﹐M(m,4),接下来依据等腰三角形的性质可得到PM=EM,从而得到关于m的方程,于是可求得点P的坐标.
②作PN⊥BC,垂足为N.先证明△PNE![]() △COB,由相似三角形的性质可知PN与PE的关系,然后再证明△PFN
△COB,由相似三角形的性质可知PN与PE的关系,然后再证明△PFN![]() △CAF,由相似三角形的性质可得到PF:AF与m的函数关系式,从而可求得
△CAF,由相似三角形的性质可得到PF:AF与m的函数关系式,从而可求得![]() 最大值.
最大值.
(1)设抛物线的解析式为y=a(x+2)(x﹣8).
∵抛物线经过点C(0,4),
∴﹣16a=4,解得a=﹣![]() .
.
∴抛物线的解析式为y=﹣![]() (x+2)(x﹣8)=
(x+2)(x﹣8)=![]() x2+
x2+![]() x+4.
x+4.
∵A(﹣2,0)、B(8,0),
∴抛物线的对称轴为x=3.
∵将x=3代入得:y=![]() ,
,
∴抛物线的顶点D坐标为(3,![]() ).
).
(2)三角形ABC是直角三角形,理由如下:
∵AB=10,AC=2,BC=4![]() ,
,
∴AC2+BC2=AB2.
∴∠BCA=90°,所以三角形ABC是直角三角形.
(3) ①如图1所示:作CM⊥PE,垂足为M.
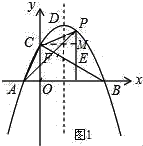
设直线BC的解析式为y=kx+b.
∵将B、C的坐标代入得:![]() ,解得k=﹣
,解得k=﹣![]() ,b=4,
,b=4,
∴直线BC的解析式为y=﹣![]() x+4.
x+4.
设点P(m,﹣ ![]() m2+
m2+![]() m+4),则点E(m,﹣
m+4),则点E(m,﹣![]() m+4),M(m,4).
m+4),M(m,4).
∵PC=EC,CM⊥PE,
∴PM=EM.
∴﹣![]() m2+
m2+![]() m+4﹣4=4﹣(﹣
m+4﹣4=4﹣(﹣![]() m+4),解得:m=0(舍去),m=4.
m+4),解得:m=0(舍去),m=4.
∴P(4,6).
②作PN⊥BC,垂足为N.

由①得:PE=﹣![]() m2+2m.
m2+2m.
∵PE∥y轴,PN⊥BC,
∴∠PNE=∠COB=90°,∠PEN=∠BCO.
∴△PNE∽△BOC.
∴![]() =
=![]() .
.
∴PN=![]() PE=
PE=![]() (﹣
(﹣![]() m2+2m).
m2+2m).
由(2)知∠BCA=90°,
又∵∠PFN=∠CFA,
∴△PFN∽△CAF.
∴ =﹣
=﹣![]() m2+
m2+![]() m.
m.
∴当m=4时,![]() 的最大值为
的最大值为![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿着折线
的速度沿着折线![]() 运动,到达点
运动,到达点![]() 时停止运动;点
时停止运动;点![]() 从点
从点![]() 出发,也以
出发,也以![]() 的速度沿着折线
的速度沿着折线![]() 运动,到达点
运动,到达点![]() 时停止运动.点
时停止运动.点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() .
.
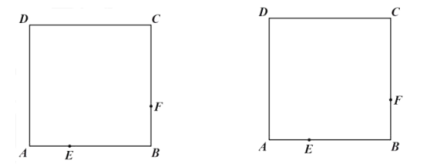
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
(2)连接![]() 、
、![]() 交与点
交与点![]() ,
,
①在整个运动过程中,![]() 的最小值为______
的最小值为______![]() ;
;
②当![]() 时,此时
时,此时![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
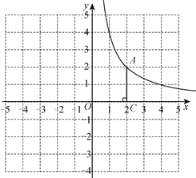
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象经过点
的图象经过点![]() ,
,![]() .
.
(1)求代数式mn的值;
(2)若二次函数![]() 的图象经过点B,求代数式
的图象经过点B,求代数式![]() 的值;
的值;
(3)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象只有一个交点,且该交点在直线
的图象只有一个交点,且该交点在直线![]() 的下方,结合函数图象,求
的下方,结合函数图象,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象经过点
的图象经过点![]() ,作AC⊥x轴于点C.
,作AC⊥x轴于点C.
(1)求k的值;
(2)直线AB:![]() 图象经过点
图象经过点![]() 交x轴于点
交x轴于点![]() .横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
.横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
①直线AB经过![]() 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;
②若区域W内恰有1个整点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图某幢大楼顶部有广告牌CD.张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进14米、站在点B处,测得广告牌顶端点C的仰角为45°.(取![]() ,计算结果保留一位小数)
,计算结果保留一位小数)

(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
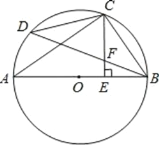
【题目】如图,AB 是⊙O 的直径,C 是![]() 的中点,CE⊥AB 于点 E,BD 交CE 于点 F.
的中点,CE⊥AB 于点 E,BD 交CE 于点 F.
(1)求证:CF=BF;
(2)若 CD=6,AC=8,求⊙O 的半径及 CE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5,它们除了数字外没有任何区别.
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果。现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜。请问这样的游戏规则对甲乙双方公平吗?请说明理由。若不公平,请修改该游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线.
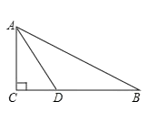
(1) 用无刻度的直尺和圆规过A、D两点作⊙O,使圆心O在AB边上 (保留画图痕迹,不写画法)
(2) 求证:BC为⊙O的切线;
(3) 如果AC=3,tanB=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
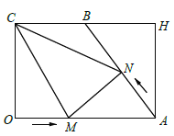
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() . 动点
. 动点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 运动,两个动点同时出发,速度都是每秒1个单位长度,连接
运动,两个动点同时出发,速度都是每秒1个单位长度,连接![]() ,设运动时间为
,设运动时间为![]() (秒)
(秒)![]() . 则
. 则![]() _____时,
_____时,![]() 为直角三角形
为直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com