
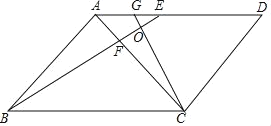
【题目】如图,ABCD中,∠BAC=90°,AB=AC,点E是边AD上一点,且BE=BC,BE交AC于点F,过点C作BE的垂线,垂足为点O,与AD交于点G.
(1)若AB=![]() ,求AE的长;
,求AE的长;
(2)求证;BF=CO+![]() EO.
EO.
【答案】(1)AE=![]() ﹣1;(2)证明见解析.
﹣1;(2)证明见解析.
【解析】
(1)过E作EH⊥BA交BA的延长线于于H,根据等腰直角三角形的性质得到∠ABC=45°,BC=BE=2,根据平行线的性质得到∠HAE=∠ABC=45°,设AH=HE=a,得到AE=![]() a,根据勾股定理即可得到结论;
a,根据勾股定理即可得到结论;
(2)由(1)知,∠OBC=30°,得到BF=OB﹣OF=![]() OC﹣OE,过G作GH⊥BC于H,求出OE=(2﹣
OC﹣OE,过G作GH⊥BC于H,求出OE=(2﹣![]() )OC,把OE=(2﹣
)OC,把OE=(2﹣![]() )OC代入
)OC代入![]() OC﹣OE求得BF=2(
OC﹣OE求得BF=2(![]() ﹣1)OC,代入求得CO+
﹣1)OC,代入求得CO+![]() EO=2(
EO=2(![]() ﹣1)OC,于是得到结论.
﹣1)OC,于是得到结论.
解:(1)过E作EH⊥BA交BA的延长线于于H,
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,BC=BE=2,
∵AD∥BC,
∴∠HAE=∠ABC=45°,
∴设AH=HE=a,
∴AE=![]() a,
a,
在Rt△EBH中,∵BH2+EH2=BE2,
∴(a+![]() )2+a2=22,
)2+a2=22,
∴a=![]() ,
,
∴AE=![]() ﹣1;
﹣1;
(2)过A作AM⊥BC于M,GH⊥BC于H,EN⊥BC于N,
则AM=GH=EN=![]() BC=1,
BC=1,
∴sin∠EBC=![]() ,
,
∴∠EBC=30°,
∴OC=![]() BC=1,
BC=1,
∴∠OBC=30°,
∵BE=BC,
∴∠BEC=75°,
∵∠CFE=45°+30°=75°,
∴CF=CE,
∴OF=OE,
∵OC⊥BO,
∴BO=![]() OC,
OC,
∴BF=OB﹣OF=![]() OC﹣OE,
OC﹣OE,
过G作GH⊥BC于H,
∴GH=EN=OC=![]() CG=
CG=![]() (OC+OG)=
(OC+OG)=![]() (OC+
(OC+![]() OE),
OE),
∴OC=![]() (OC+
(OC+![]() OE),
OE),
∴OE=(2﹣![]() )OC,
)OC,
∴BF=OB﹣OF=![]() OC﹣OE=2(
OC﹣OE=2(![]() ﹣1)OC,
﹣1)OC,
∵CO+![]() EO=OC+
EO=OC+![]() (2﹣
(2﹣![]() )OC=2(
)OC=2(![]() ﹣1)OC,
﹣1)OC,
∴BF=CO+![]() EO.
EO.



 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
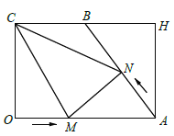
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() . 动点
. 动点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 运动,两个动点同时出发,速度都是每秒1个单位长度,连接
运动,两个动点同时出发,速度都是每秒1个单位长度,连接![]() ,设运动时间为
,设运动时间为![]() (秒)
(秒)![]() . 则
. 则![]() _____时,
_____时,![]() 为直角三角形
为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
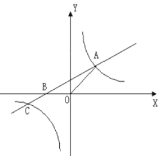
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 交于点
交于点![]() ,其中点
,其中点![]() 在第一象限,点
在第一象限,点![]() 在第三象限。
在第三象限。
(1)求双曲线的解析式;
(2)求![]() 点的坐标;
点的坐标;
(3)若![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,请写出
是等腰三角形?若存在,请写出![]() 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜂蜜具有消食、润肺、安神、美颜之功效,是天然的健康保健佳品.秋天即将来临时,雪宝山土特产公司抓住商机购进甲、乙、丙三种蜂蜜,已知销售每瓶甲蜂蜜的利润率为10%,每瓶乙蜂蜜的利润率为20%,每瓶丙蜂蜜的利润率为30%.当售出的甲、乙、丙蜂蜜瓶数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙蜂蜜瓶数之比为3:2:1时,商人得到的总利润率为20%.那么当售出的甲、乙、丙蜂蜜瓶数之比为5:6:1时,该公司得到的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中的三个顶点在⊙
中的三个顶点在⊙![]() 上,
上,![]() 是优弧
是优弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合).
重合).
(1)当圆心![]() 在
在![]() 内部,
内部,![]() 时,
时,![]() ________.
________.
(2)当圆心![]() 在
在![]() 内部,四边形
内部,四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的度数;
的度数;
(3)当圆心![]() 在
在![]() 外部,四边形
外部,四边形![]() 为平行四边形时,请直接写出
为平行四边形时,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的![]() .在销售过程中发现,这种儿童玩具每天的销售量
.在销售过程中发现,这种儿童玩具每天的销售量![]() (件
(件![]() 与销售单价
与销售单价![]() (元
(元![]() 满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.
满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.
(1)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
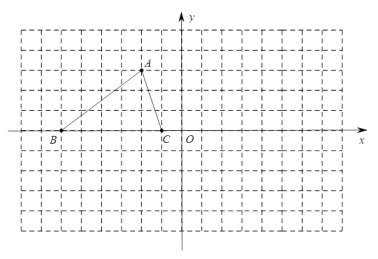
(1)点A关于y轴对称的点的坐标是 ;
(2)将△ABC绕坐标原点O顺时针旋转180°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是⊙O的直径,点C在AB的延长线上,AB=4,BC=2,P是⊙O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.
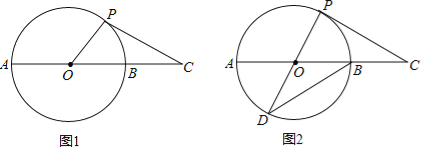
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com