
分析 过点A作AD⊥BC,利用勾股定理求出AD的长,再利用三角形的面积公式求出△ABC的面积即可.
解答 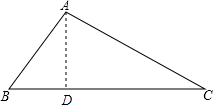 解:过点A作AD⊥BC.
解:过点A作AD⊥BC.
设BD=x,则CD=21-x,
在Rt△ABD中,AD2=102-x2,
在Rt△ADC中,AD2=172-(21-x)2,
∴102-x2=172-(21-x)2,
100-x2=289-441+42x-x2,
解得x=6,
∴CD=15,
在Rt△ACD中,AD=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴△ABC的面积=$\frac{1}{2}$×BC•AD=$\frac{1}{2}$×21×8=84.
故答案为:84.
点评 本题考查了勾股定理,解决本题的关键在于利用两个直角三角形的公共边找到突破点.主要利用了勾股定理进行解答.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:初中数学 来源: 题型:填空题
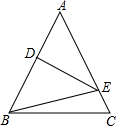 如图△ABC中,AB=AC,DE⊥AB,D是AB的中点,DE交AC于E点,连结BE,BC=10cm,
如图△ABC中,AB=AC,DE⊥AB,D是AB的中点,DE交AC于E点,连结BE,BC=10cm,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 出生年份 | 2022年年龄(岁) | 延迟退休时间(年) | 实际退休年龄(岁) |
| 1967 | 55 | 0.5 | 55.5 |
| 1968 | 54 | 1 | 56 |
| 1969 | 53 | 1.5 | 56.5 |
| 1970 | 52 | 2 | 57 |
| 1971 | 51 | 2.5 | 57.5 |
| 1972 | 50 | 3 | 58 |
| … | … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,由1开始连续自然数组成,观察规律,并完成以下各题.
如图所示,由1开始连续自然数组成,观察规律,并完成以下各题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)| A. | x | B. | 180°-2x | C. | 180°-x | D. | 2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com