
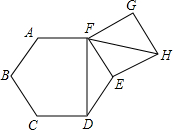
 如图,在正六边形ABCDEF的外侧,作正方形EFGH,则∠DFH的度数为
如图,在正六边形ABCDEF的外侧,作正方形EFGH,则∠DFH的度数为 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 某车间周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
某车间周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -15 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
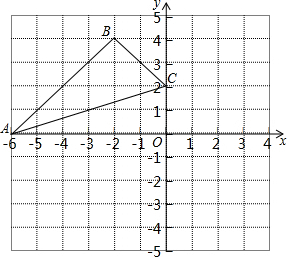 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件:
如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件:查看答案和解析>>
科目:初中数学 来源: 题型:
| 1-x |
| x-2 |
| 1 |
| 2-x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com