
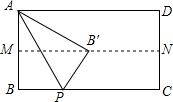
 如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )
如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )| A. | 30° | B. | 45° | C. | 60° | D. | 无法确定 |
分析 根据矩形的性质及折叠的性质得出AB′=2AM,从而利用含30°角的直角三角形的性质和翻折的性质得到∠APB=30°,再根据直角三角形的性质即可得出答案.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD,∠B=90°,
∵M、N分别为AB、CD的中点,
∴AM=$\frac{1}{2}$AB,∠AMB′=90°,
由折叠的性质得:AB′=AB=2AM,
∴∠AB′M=30°,
∴∠BAB′=60°,
∴∠BAP=30°,
∴∠APB=60°.
故选:C.
点评 此题考查了翻折变换的知识,涉及了含30°角的直角三角形的性质,解答本题的关键是求出∠AB′M=30°,这是解答问题的突破口.


科目:初中数学 来源: 题型:填空题
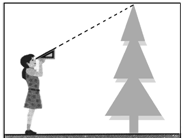 小莉站在离一棵树水平距离为2米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为($\frac{2\sqrt{3}}{3}$+1.5)米.(结果保留根号)
小莉站在离一棵树水平距离为2米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为($\frac{2\sqrt{3}}{3}$+1.5)米.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
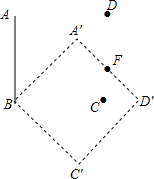 如图所示,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A′BC′D′.在这个旋转过程中:
如图所示,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A′BC′D′.在这个旋转过程中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com