
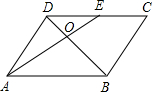
 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,它正在播放动画片 | |
| B. | 播下一颗种子,种子一定会发芽 | |
| C. | 买100张中奖率为1%的彩票一定会中奖 | |
| D. | 太阳从东方升起 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
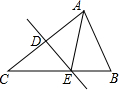 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )| A. | 10 | B. | 13 | C. | 16 | D. | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com