Question

【题目】如图，在Rt△ABC中，∠BAC＝90°，AB＞AC ， 射线AM平分∠BAC ．

（1）设AM交BC于点D ， 作DE⊥AB于点E ， DF⊥AC于点F ， 连接EF ． 有以下三种“判断”：
判断1：AD垂直平分EF．
判断2：EF垂直平分AD．
判断3：AD与EF互相垂直平分．
你同意哪个“判断”？简述理由；
（2）若射线AM上有一点N到△ABC的顶点B ， C的距离相等，连接NB ， NC ．
①请指出△NBC的形状，并说明理由；
②当AB＝11，AC＝7时，求四边形ABNC的面积．

Answer 1

【答案】
（1）

解：判断3.理由如下：如图，

∵DE⊥AB于点E，DF⊥AC于点F， ∠BAC＝90°，

∴四边形AEDF是矩形，

又∵射线AM平分∠BAC，

∴∠DAE=∠DAF，

又∵AEDF是矩形，

∴AF//DE，

∴∠DAF=∠EDA。

∴∠EDA=∠DAE，

则AE=DE，

则矩形AEDF是正方形。

即AD与EF互相垂直平分．

（2）

解：①等腰直角三角形.理由如下：

作NE⊥AB于点E，NF⊥AC于点F，

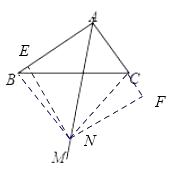
由（1）可得四边形AENF是正方形，

∴NE=NF，∠ENF=∠NEA=∠NFC=90°，

∴∠NEB=∠NFC=90°，

又NB=NC，

则△NBE≌△NCF，

∴∠BNE=∠CNF，

∴∠BNC=∠ENF=90°，

∴△NBC是等腰直角三角形.

②在Rt△ABC中，由勾股定理得BC=.

在Rt△NBC中，∵NB=NC，BC=，

则NB=NC==，

则四边形ABNC的面积=S△ABC+S△NBC=×11×７＋××＝×162=81.

【解析】（1）判断四边形AEDF为正方形，即可证明；
（2）①根据（1）中的方法作出两条垂线，则可证得NE=NF，∠ENF=∠NEA=∠NFC=90°，再证明△NBE≌△NCF，通过等量代换，证明∠BNC=∠ENF=90°；
②由勾股定理求出△NBC直角边的长度分别计算S△ABC和S△NBC即可求得答案.
【考点精析】关于本题考查的等腰直角三角形和勾股定理的概念，需要了解等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．