
【题目】丽君花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若一次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数解析式;
(2)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少费用是多少元?
【答案】(1)太阳花:![]() ,绣球花:y=
,绣球花:y=![]() ;(2)太阳花30盆,绣球花60盆时,总费用最少,最少费用是700元.
;(2)太阳花30盆,绣球花60盆时,总费用最少,最少费用是700元.
【解析】
试题分析:(1)直接求出太阳花的付款金额y(元)关于购买量x(盆)的函数解析式;绣球花的付款金额分两种情况讨论:①一次购买的绣球花不超过20盆;②一次购买的绣球花超过20盆;
(2)太阳花数量不超过绣球花数量的一半,可得太阳花数量不超过两种花数量的![]() ,即太阳花数量不超过30盆,所以绣球花的数量不少于60盆;然后设太阳花的数量是x盆,则绣球花的数量是90﹣x盆,求出购买两种花的总费用是多少,进而判断出两种花卉各买多少盆时,总费用最少,最少费用是多少元即可.
,即太阳花数量不超过30盆,所以绣球花的数量不少于60盆;然后设太阳花的数量是x盆,则绣球花的数量是90﹣x盆,求出购买两种花的总费用是多少,进而判断出两种花卉各买多少盆时,总费用最少,最少费用是多少元即可.
试题解析:(1)太阳花的付款金额y(元)关于购买量x(盆)的函数解析式是:![]() ;
;
①一次购买的绣球花不超过20盆时,付款金额y(元)关于购买量x(盆)的函数解析式是:![]() (x≤20);
(x≤20);
②一次购买的绣球花超过20盆时,付款金额y(元)关于购买量x(盆)的函数解析式是:y=10×20+10×0.8×(x﹣20)=200+8x﹣160=8x+40,
综上,可得绣球花的付款金额y(元)关于购买量x(盆)的函数解析式是:y=![]() ;
;
(2)根据题意,可得太阳花数量不超过:90×![]() =30(盆),所以绣球花的数量不少于:90﹣30=60(盆),设太阳花的数量是x盆,则绣球花的数量是90﹣x盆,购买两种花的总费用是y元,则x≤30,则y=6x+[8(90﹣x)+40]=760﹣2x,因为x≤30,所以当x=30时,
=30(盆),所以绣球花的数量不少于:90﹣30=60(盆),设太阳花的数量是x盆,则绣球花的数量是90﹣x盆,购买两种花的总费用是y元,则x≤30,则y=6x+[8(90﹣x)+40]=760﹣2x,因为x≤30,所以当x=30时,![]() =760﹣2×30=700(元),即太阳花30盆,绣球花60盆时,总费用最少,最少费用是700元.
=760﹣2×30=700(元),即太阳花30盆,绣球花60盆时,总费用最少,最少费用是700元.
答:太阳花30盆,绣球花60盆时,总费用最少,最少费用是700元.


科目:初中数学 来源: 题型:
【题目】我们知道有两条边相等的三角形叫做等腰三角形.类似的,我们定义:至少有一组对边相等的四边形叫做等对边四边形.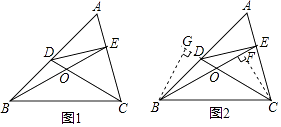
(1)请写出一个你学过的四边形中是等对边四边形的图形的名称.
(2)如图1,在△ABC中,点D、E分别在AB、AC上,且CD、BE相交于点O,若∠A=60°,∠DCB=∠EBC= ![]() ∠A.请你写出与∠A相等的角.
∠A.请你写出与∠A相等的角.
(3)我们易证图中的四边形BCED是等对边四边形.
(提示:如图2,可证△BGO≌△CFO再证△BGD≌△CFE,可得到结论BD=CE.不需证明)
若在△ABC中,如果∠A是不等于60°的锐角,D、E分别在AB、AC上,且CD、BE相交于点O,∠DCB=∠EBC= ![]() ∠A.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
∠A.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
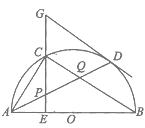
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:
的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:
①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.
其中正确结论是________ (只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“﹣”表示成绩小于14秒
﹣1 | +0.8 | 0 | ﹣1.2 | ﹣0.1 | 0 | +0.5 | ﹣0.6 |
(1)求这个小组的男生达标率是多少?
(2)求这个小组8名男生的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=30cm.
(1)如图1,点P沿线段AB自点A向点B以2cm/s的速度运动,同时点Q沿线段BA自点B向点A以3cm/s的速度运动,几秒钟后,P、Q两点相遇?
(2)几秒后,点P、Q两点相距10cm?
(3)如图2,AO=PO=4cm,∠POB=60°,现点P绕着点O以30°/秒的速度逆时针旋转一周停止,同时点Q沿直线自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.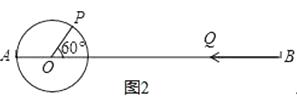
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后分钟,甲乙两人第一次走在同一条边上. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com