
【题目】如图,在直角△ABC中,∠ACB=90°,AC=3,BC=4,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD于M,EN⊥DC于N.
(1)当AD=CD时,求证DE//AC;
(2)当∠MBE与△CNE的某一个内角相等时,求AD的长;
(3)当四边形MEND与△BDE的面积相等时,求AD的长.

【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由等腰三角形的性质得出∠A=∠DCA,由三角形的外角性质和角平分线得出得出∠C=∠BDE,即可得出结论;(2)存在以下两种情况①当∠B=∠ECN时;②当∠B=∠CNE时,根据相似三角形的性质即可求得;(3)根据四边形MEND与△BDE的面积相等,得到△DME与△BME的面积相等.证明△BME∽△BCA,△CDE∽△CBD,即可解答.
试题解析:
(1)证明:∵AD=CD,
∴∠A=∠ACD.
∵∠CDB=∠A+∠ACD,
∴∠CDB=2∠A.
∵DE平分∠CDB,
∴∠BDE=![]() ∠CDB=∠A.
∠CDB=∠A.
∴DE∥AC.
(2)∵∠ACB=90°,AC=3,BC=4,
∴AB=5.
∵EM⊥BD,EN⊥CD,
∴∠BME=∠CNE=90°.
存在以下两种情况
①当∠B=∠ECN时
∴CD=BD,
∵∠B+∠A=90°,∠ECN+∠ACD=90°,
∴∠A=∠ACD.
∴CD=AD.
∴AD=BD=![]() .
.
②当∠B=∠CNE时
∴NE∥AB.
∴∠ADC=∠CNE=90°.
∴∠ADC=∠ACB.
∵∠A=∠A,
∴△ACD∽△ABC,
∴![]() .
.
∴![]() .
.
(3)∵∠EDN=∠EDM,∠DNE=∠DME=90°,DE=DE,
∴△DNE≌△DME.
∵四边形MEND与△BDE的面积相等,
∴△DME与△BME的面积相等.
∴DM=BM.
∵EM⊥BD,
∴DE=BE.
∴∠B=∠BDE=∠CDE.
∵∠B=∠B,∠BME=∠ACB=90°,
∴△BME∽△BCA.
∴![]() .
.
∴![]() .
.
∵∠DCE=∠DCB,
∴△CDE∽△CBD.
∴![]() .
.
∴CD=![]() .
.
∴CE=![]() .
.
∴BD=![]() .
.
∴BE=![]() .
.
∴AD=AB-BD=5-![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( ) 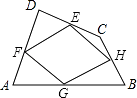
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列哪些线段能组成三角形( )
①3cm、3cm、5cm ②3cm、3cm、3cm ③2cm、2cm、4cm ④3cm、5cm、9cm
A.①②B.③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.明天是晴天
B.有一匹马的奔跑速度是100米/秒
C.打开电视正在播广告
D.在地面上向空中抛掷一石块,石块终将落下
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.同圆或等圆中弧相等,则它们所对的圆心角也相等
B.90°的圆心角所对的弦是直径
C.平分弦的直径垂直于这条弦
D.三点确定一个圆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com