
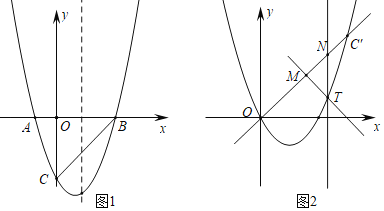
����Ŀ����ͼ1��������y��ax2+bx+c��x�ύ�ڵ�A(��1��0)��B(3��0)����y�ύ�ڵ�C(0����3).
(1)�������ߵĽ���ʽ��
(2)���������Ƿ����һ��P��ʹ�á�APB����ACO�����������ڣ������P�����꣺�������ڣ���˵������.
(3)���ǹ涨������ֱ��l1��y��k1x+b��ֱ��l2��y��k2x+b2����ֱ��k1k2����1����ֱ��l1��l2��������Ҳ����.���������涨������п��⣺
��ͼ2����������������ƽ�ƹ�ԭ����ֱ��y��kx(k��0)������C��.��TΪ�ö��κ���ͼ����λ��ֱ��OC�·��Ķ��㣬����T��ֱ��TM��OC��������Ϊ��M����M���߶�OC����(����O��C���غ�)������T��ֱ��TN��y�ύOC'�ڵ�N.���ڵ�T�˶��Ĺ����У�![]() Ϊ��������ȷ��k��ֵ.
Ϊ��������ȷ��k��ֵ.
���𰸡�(1)y��x2��2x��3��(2)���ڣ���P(��![]() ��
��![]() ��(��
��(��![]() ����
����![]() )��(3)k��
)��(3)k��![]() .
.
��������
(1)�����ߵı���ʽΪ��y��a(x+1)(x��3)��a(x2��2x��3)��������⣻
(2)�ֵ�P��x���Ϸ�����P��x���·�����������ֱ���⼴�ɣ�
(3)OM��![]() ��
��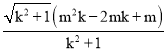 ��ON��m
��ON��m![]() ���������.
���������.
�⣺(1)�����ߵı���ʽΪ��y��a(x+1)(x��3)��a(x2��2x��3)��
����3a����3����ã�a��1��
�������ߵı���ʽΪ��y��x2��2x��3������
(2)tan��APB��tan��ACO��![]() ��
��
������P��x���Ϸ�ʱ��
��ֱ��BP�ı���ʽΪ��y����![]() x+1������
x+1������
�����٢�����ã�x��3(��ȥ)��![]() ���ʵ�P(��
���ʵ�P(��![]() ��
��![]() )��
)��
������P��x���·�ʱ��
ͬ���ɵã���P(��![]() ����
����![]() )��
)��
���ϣ���P(��![]() ��
��![]() ��(��
��(��![]() ����
����![]() )��
)��
(3)���T(m��m2��2m)��ֱ��ON�ı���ʽΪ��y��kx������
��TM��OC����ֱ��TMΪ��y����![]() x+b��
x+b��
����T�����������ʽ����ã�
ֱ��TM�ı���ʽΪ��y����![]() x+(m2��2m+
x+(m2��2m+![]() )������
)������
�����ۢ�����ã�x��![]() ��y��
��y��![]() ��
��
��OM��![]() ��
��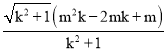 ��ON��m
��ON��m![]() ��
��
![]() ��
��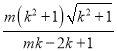 ��
��
��k��![]() ʱ��
ʱ��![]() ��
��![]() ����.
����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AC��CD��BE�ֱ��ǡ�ABC�Ľ�ƽ���ߣ�AG��BC��AG��BG�����н��ۣ��١�BAG��2��ABF����BAƽ�֡�CBG���ۡ�ABG����ACB���ܡ�CFB��135����������ȷ�Ľ����У���������
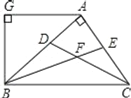
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��5��14����15������һ��һ·�����ʺ����߷���̳�ڱ������У�������̳�ڼ䣬�й�ͬ30��������ǩ��ó����Э�飬ij���������ס���������Ʒ��8����������һ��һ·�����߹��Һ͵�������֪2��������Ʒ��3��������Ʒ������������ͬ��3��������Ʒ��2��������Ʒ������������1500Ԫ.
(1)������Ʒ��������Ʒ�����۵��۸�����Ԫ��
(2)���ס���������Ʒ�����������벻����5400��Ԫ�����������ۼ�����Ʒ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ����Ժ��ָʾ����ij�ط�������̨��һϵ������ũ���Ż����ߣ�ʹũ�������������ӣ�ijũ����������һ��ũ��Ʒ����֪���ֲ�Ʒ�ijɱ���Ϊÿǧ��20Ԫ���г����鷢�֣��ò�Ʒÿ���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ������¹�ϵ��y=��2x+80�������ֲ�Ʒÿ�����������ΪwԪ��
��1����w��x֮��ĺ�����ϵʽ��
��2���ò�Ʒ���ۼ۶�Ϊÿǧ�˶���Ԫʱ��ÿ����������������������Ƕ���Ԫ��
��3�������۲��Ź涨���ֲ�Ʒ�����ۼ۲�����ÿǧ��28Ԫ����ũ����Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊÿǧ�˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC����ACB��90����AC��BC��4.D��AB���е㣬P��ƽ���ϵ�һ�㣬��DP��1������BP��CP������B�Ƶ�P˳ʱ����ת90���õ���B������CB����CB�������ֵ��_____.
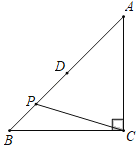
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ��b�dz�������
��b�dz�������![]() ��0����x�ύ��A��B���㣬��y�ύ�ڵ�C������A��B���������ֱ���A(��1��0)��B(3��0)
��0����x�ύ��A��B���㣬��y�ύ�ڵ�C������A��B���������ֱ���A(��1��0)��B(3��0)
��1�����������ߵĽ���ʽ���ڶ���D������Ϊ_______����ֱ��BD�Ľ���ʽΪ______��
��2����PΪ�߶�BD�ϵ�һ�����㣬�������Ϊm������P��PQ��x���ڵ�Q����mΪ��ֵʱ���ı���PQOC��������
��3������M���������ڵ�һ�����ϵ�һ�����㣬����M��MN��AC��![]() ���ڵ�N������M������Ϊ_______ʱ���ı���MNAC��ƽ���ı��Σ�
���ڵ�N������M������Ϊ_______ʱ���ı���MNAC��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
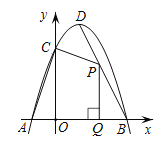
����Ŀ����ͼ��������y=��x2+bx+c������A(��3��0)����C(0��3)����DΪ���κ����Ķ��㣬DEΪ���κ����ĶԳ��ᣬ��E��x���ϣ�
��1���������ߵĽ���ʽ������D�����ꣻ
��2����������A��C����֮����һ��F��ʹ��FAC����������F�����ꣻ
��3��ֱ��DE���Ƿ���ڵ�P��ֱ��AD�ľ����뵽x��ľ�����ȣ������ڣ��������P���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD��,��BAD=60��,AC=12,E���߶�AD�ӳ�����һ��,����A,C,E��ֱ��������,��AE�ij�����______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ����
��ͼ����![]() (1��0).
(1��0).
(1)��![]() ,
,![]() ʱ������κ����Ľ���ʽ�����κ�����Сֵ��
ʱ������κ����Ľ���ʽ�����κ�����Сֵ��
(2)���κ�����ͼ����![]() (
(![]() ,
,![]() )��
)��![]() (
(![]() ��
��![]() ).��������ʵ��
).��������ʵ��![]() ������ֵ
������ֵ![]() ����С��
����С��![]() �����ʱ���κ����Ľ���ʽ.
�����ʱ���κ����Ľ���ʽ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com