
【题目】计算:
(1)计算:![]()
(2)化简:![]()
(3)化简:![]()
(4)化简求值:![]() ,其中x=1009,y=
,其中x=1009,y=![]()
【答案】(1)-6;(2)![]() ;(3)
;(3)![]() ;(4)-xy,
;(4)-xy,![]() .
.
【解析】
(1)原式利用乘方的意义,零指数幂、负整数指数幂法则计算即可得到结果;
(2)原式先利用同底数幂的乘法,积的乘方及幂的乘方运算法则计算,再合并同类项即可得到结果;
(3)原式利用完全平方公式及平方差公式化简即可得到结果.
(4)首先利用平方差公式计算,然后合并同类项,最后利用多项式除以单项式的法则计算即可求解.
(1)![]()
![]()
= -6;
(2)![]()
=![]()
=![]() ;
;
(3)![]()
= ![]()
=![]()
=![]() ;
;
(4)[(xy+2)(xy-2)-2x2y2+4]÷(xy)
=(x2y2-4-2x2y2+4)÷xy
= -xy,
当x=1009,y=![]() 时,原式=
时,原式=![]() =
=![]() .
.
故答案为:(1)-6;(2)![]() ;(3)
;(3)![]() ;(4)-xy,
;(4)-xy,![]() .
.


科目:初中数学 来源: 题型:
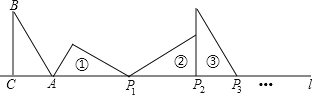
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,且AC在直线1上,将△ABC绕点A顺时针旋转到位置①,可得到点P1,将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,…,按此规律继续旋转,得到点P2018为止,则AP2018=___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.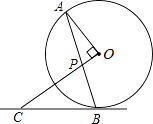
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为 ![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
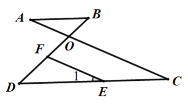
【题目】如图,AC与BD相交于点O,点E是CD上的一点,F是OD上的一点,且EF∥AC,∠1=∠A.
(1)求证:AB∥CD.
(2)若∠BFE=70°,求:∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.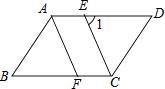
查看答案和解析>>
科目:初中数学 来源: 题型:
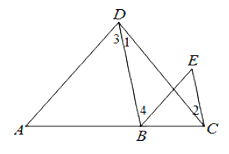
【题目】按图填空,并注明理由.
已知: 如图,∠1=∠2,∠3=∠E. 求证:AD∥BE.
证明: ∵∠1=∠2 (已知)
∴ BD ∥ ( )
∴ ∠E = ( )
又 ∵ ∠E=∠3 ( 已知 )
∴ ∠3=∠ ( )
∴ AD∥BE.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
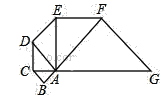
【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com