Question

7．如图，?ABCD中，BE⊥AD于点E，且点E为AD的中点，AD=BE=4，点P从点A出发以每秒1个单位长度的速度沿射线AD方向运动，设点P的运动时间为t秒，点P出发后过点P作AD的垂线，交折线AB-BC于点Q，以PQ为边向左作正方形PQMN．

（1）直接写出点N与点D重合时，t的值．
（2）当0≤t≤2时，用含t的代数式表示线段EN的长．
（3）如图②，当0≤t≤2时，设点O为BE的中点，请直接写出△OQM为等腰三角形时，t的值．

Answer 1

分析 （1）先求得tan∠A=2．从而得到PA=t，PD=QP=2t，最后依据PA+PN=4列方程求解即可；
（2）①当0＜t＜$\frac{2}{3}$时，EN=AE-PA-PN；当$\frac{2}{3}$≤t＜2时，EN=AN-AE=PA+PN-AE；
（3）如图4所示：建立坐标系可得到Q（2-t，2t，），M（2-3t，2t），然后分为OM=OQ，MO=MQ，QO=QM三种情况，接下来依据两点间的距离公式列方程求解即可．

解答 解：（1）如图1所示：
∵E是AD的中点，AD=4，
∴AE=2．
∵AE=2，BE=4，∠BEA=90°，
∴tan∠A=2．
又∵PA=t，
∴QP=2t．
∵PQMN为正方形，
∴PD=2t．
∴t+2t=4．
解得：t=$\frac{4}{3}$．

（2）①当0＜t＜$\frac{2}{3}$时，如图2所示：
∵由（1）可知PA=t，NP=2t．
∴EN=AE-PA-PN=2-t-2t=2-3t．
当$\frac{2}{3}$≤t＜2时，如图3所示：
∵由（1）可知PA=t，NP=2t．
∴EN=AN-AE=PA+PN-AE=t+2t-2=3t-2．
综上所述，EN=$\left\{\begin{array}{l}{2-3t（0＜t＜\frac{2}{3}）}\\{3t-2（\frac{2}{3}≤t＜2）}\end{array}\right.$．
（3）如图4所示：
∵PA=t，PQ=QM=2t，
∴Q（2-t，2t，），M（2-3t，2t）．
当OM=OQ时，由两点间的距离公式可知：（2-3t）²+（2-2t）²=（2-t）²+（2-2t）²．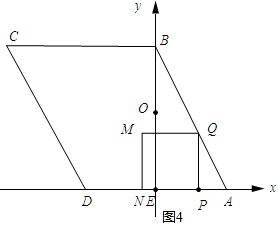
整理得：-2t（4-4t）=0．
解得：t=1或t=0（舍去）．
当MO=MQ时．（2-3t）²+（2-2t）²=（2t）²．
整理得：9t²-20t+8=0．
解得：t=$\frac{10+2\sqrt{7}}{9}$或t=$\frac{10-2\sqrt{7}}{9}$．
当QO=QM时（2-t）²+（2-2t）²=（2t）²．
整理得：t²-12t+8=0．
解得：t=6-2$\sqrt{7}$，t=6+2$\sqrt{7}$（舍去）．
综上所述，当t=6-2$\sqrt{7}$或t=$\frac{10+2\sqrt{7}}{9}$或t=$\frac{10-2\sqrt{7}}{9}$时，△MQO为等腰三角形．

点评 本题主要考查的是四边形的综合应用，解答本题主要应用了锐角三角形函数的定义、正方形的性质、正方形的面积、梯形的面积、三角形的面积，等腰三角形的定义，两点间的距离公式、一元二次方程、一元一次方程的解法，根据题意画出符合题意的图形是解题的关键．